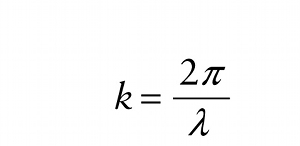Angular wave number (13-5)

Review

The quantity $2pi{f}$ is the angular frequency $\omega$ of the wave (see Equations 13-1), and the combination $2\pi/\lambda$ in Equation 13-4 is called the $\textbf{angular wave number}$. We use the symbol $k$ for this quantity:

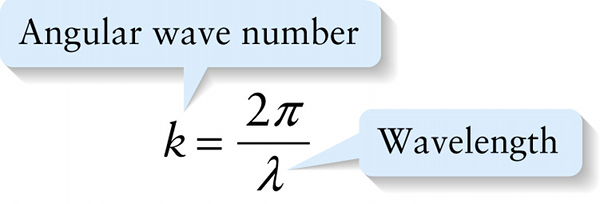
Since $2\pi$ represents the number of radians in one cycle and wavelength $\lambda$ is in meters, the angular wave number $k$ is measured in radians per meter (rad/m). We use the adjective $\textit{angular}$ since the term "wave number" is typically used for $1/\lambda$, the reciprocal of the wavelength. This quantity multiplied by $2\pi$ is the angular wave number $k = 2\pi{f}$.