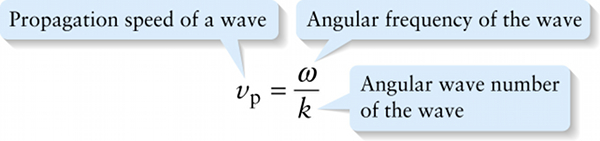Propagation speed, angular frequency, and angular wave number (13-7)

Question 1 of 3

Question

Angular wave number of the wave

{"title":"Propagation speed of a wave","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"1,51,36,88\"}]"} {"title":"Angular frequency of the wave","description":"Wrong","type":"incorrect","color":"#993300","code":"[{\"shape\":\"rect\",\"coords\":\"133,9,177,51\"}]"} {"title":"Angular wave number of the wave","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"130,79,163,129\"}]"}

Review

As an aid to using Equation 13-6, note that the angular frequency $\omega = 2\pi{f}$ and the angular wave number $k = 2\pi/\lambda$ are related by the propagation speed. To see this relationship, note that $f = \omega/2\pi$ and $\lambda = 2\pi/k$ . Then from Equation 13-2,

$v_{\mathrm{p}} = f\lambda = \left(\frac{\omega}{2\pi}\right)\left(\frac{2\pi}{k}\right)$