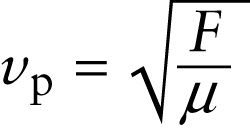Speed of a transverse wave on a rope (13-10)

Question 1 of 3

Question

Propagation speed of a transverse wave on a rope

{"title":"Propagation speed of a transverse wave on a rope","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"3,51,28,85\"}]"} {"title":"Tension in the rope","description":"Wrong","type":"incorrect","color":"#993300","code":"[{\"shape\":\"rect\",\"coords\":\"190,9,229,57\"}]"} {"title":"Mass per unit length of the rope","description":"Wrong","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"180,79,219,128\"}]"}

Review

The inertia of the rope depends on its $\textit{mass per unit length}$ or $\textbf{linear mass density}$ (SI units kg/m), which we denote by the Greek letter $\mu$ (“mu”). If the rope is uniform, $\mu$ is just equal to the mass of the rope divided by its length. A thick rope has more mass per unit length than does a piece of ordinary string and so has more inertia. As the mass per unit length of a rope increases, the wave propagation speed decreases.

If we take both restoring force and inertia into account, we find that the propagation speed $v_{\mathrm{p}}$ of a transverse wave on a rope is