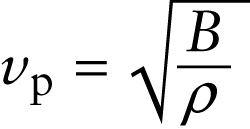Speed of a longitudinal wave in a fluid (13-11)

Review

Just as for a transverse wave on a rope, the speed of a $\textit{longitudinal}$ wave in a medium depends on the restoring force and the inertia of the medium. For a longitudinal wave in a fluid (a gas or a liquid), we call a longitudinal wave a $\textit{sound}$ wave. The disturbance associated with the wave corresponds to changes in the pressure of the fluid. We saw in Section 9-4 that the $\textit{bulk modulus}$ $B$ of a material is a measure of how it responds to pressure changes. A larger bulk modulus means the material is more difficult to compress, which means that it has a greater tendency to return to its original volume when the pressure is released. In \perpher words, the value of $B$ tells us about the restoring force that acts within a fluid when disturbed by the pressure changes associated with a longitudinal wave. A measure of the inertia of the material is its density $\rho$, equal to its mass per volume (see Example 13-3 above). A detailed analysis using Newton’s laws shows that the speed of sound waves in a fluid is

If we take both restoring force and inertia into account, we find that the propagation speed $v_{\mathrm{p}}$ of a transverse wave on a rope is

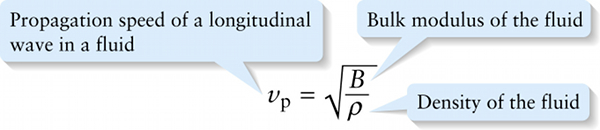
The greater the bulk modulus $B$, the faster the propagation speed; the greater the density $\rho$, the slower the propagation speed.