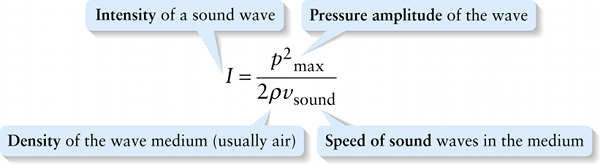
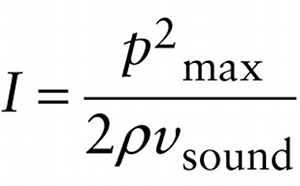Sound wave intensity in terms of pressure amplitude Pmax (13-31)

Question 1 of 4

Question

$\textbf{Density}$ of the wave medium (usually air)

{"title":"Intensity of a sound wave","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"1,67,27,115\"}]"} {"title":"Pressure amplitude of the wave","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"122,29,151,77\"}]"} {"title":"Speed of sound waves in the medium","description":"Wrong","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"155,122,183,156\"}]"} {"title":"Density of the wave medium (usually air)","description":"Correct!","type":"correct","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"116,117,152,166\"}]"}

Question

$\textbf{Speed of sound}$ waves in the medium of the wave

{"title":"Intensity of a sound wave","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"1,67,27,115\"}]"} {"title":"Pressure amplitude of the wave","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"122,29,151,77\"}]"} {"title":"Speed of sound waves in the medium","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"155,122,183,156\"}]"} {"title":"Density of the wave medium (usually air)","description":"Wrong","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"116,117,152,166\"}]"}

Question

$\textbf{Pressure amplitude}$ of the wave

{"title":"Intensity of a sound wave","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"1,67,27,115\"}]"} {"title":"Pressure amplitude of the wave","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"122,29,151,77\"}]"} {"title":"Speed of sound waves in the medium","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"155,122,183,156\"}]"} {"title":"Density of the wave medium (usually air)","description":"Wrong","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"116,117,152,166\"}]"}

Question

$\textbf{Intensity}$ of a sound wave

{"title":"Intensity of a sound wave","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"1,67,27,115\"}]"} {"title":"Pressure amplitude of the wave","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"122,29,151,77\"}]"} {"title":"Speed of sound waves in the medium","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"155,122,183,156\"}]"} {"title":"Density of the wave medium (usually air)","description":"Wrong","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"116,117,152,166\"}]"}

Review

Equation 13-29 is expressed in terms of the displacement amplitude A. However, our ears are more directly sensitive to the pressure variations in a sound wave. The displacement amplitude A in a sound wave is related to the pressure amplitude pmax, or maximum pressure variation, by

(13-30) $A = \frac{p_{\mathrm{max}}}{\rho{v_{\mathrm{sound}}}\omega}$

If we substitute Equation 13-30 for $A$ into Equation 13-29, we get an alternative expression for the intensity of a sound wave:

$I = \frac{1}{2}\rho{v_{\mathrm{sound}}\omega^2}\left(\frac{p_{\mathrm{max}}}{\rho{v_{\mathrm{sound}}}\omega}\right)^2 = \frac{p_{\mathrm{max}}^2}{2}\frac{\rho{v_{\mathrm{sound}}}\omega^2}{\rho^2v_{\mathrm{sound}}^2\omega^2}$

or, simplifying,