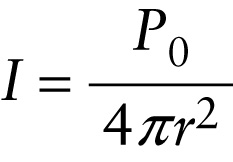Inverse-square law for sound waves (13-32)

Question 1 of 3

Question

$\textbf{Intensity}$ of a sound wave at a distance $r$ from a source that emits in all directions

{"title":"Intensity of a sound wave at a distance r from a source that emits in all directions","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"1,53,27,101\"}]"} {"title":"Power output of the sound source","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"135,8,164,56\"}]"} {"title":"Distance from the source to the point where the intensity is measured","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"170,113,198,147\"}]"}

Question

$\textbf{Power output}$ of the sound source

{"title":"Intensity of a sound wave at a distance r from a source that emits in all directions","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"1,53,27,101\"}]"} {"title":"Power output of the sound source","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"135,8,164,56\"}]"} {"title":"Distance from the source to the point where the intensity is measured","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"170,113,198,147\"}]"}

Question

$\textbf{Distance}$ from the source to the point where the intensity is measured

{"title":"Intensity of a sound wave at a distance r from a source that emits in all directions","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"1,53,27,101\"}]"} {"title":"Power output of the sound source","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"135,8,164,56\"}]"} {"title":"Distance from the source to the point where the intensity is measured","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"170,113,198,147\"}]"}

Review

Figure 13-23 shows how this comes about. Since waves carry energy, a source of sound waves is a source of energy. The rate at which the source emits energy in the form of waves is the $\textit{power}$ of the source. None of the power is lost as the waves spread away from the source, but at greater distances the power is distributed over a greater area. Hence the wave intensity (power divided by area) and the perceived loudness of the sound both decrease with increasing distance. If the source has power $P_0$ and emits equally in all directions as shown in Figure 13-23, at a distance r from the source the power is spread uniformly over a spherical surface of radius $r$ . The area of such a surface is $4\pi{r^2}$ , so the intensity equals