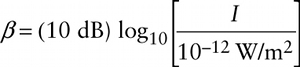Sound intensity level (13-33)

Question 1 of 3

Question

Reference intensity

{"title":"Sound intensity level of a sound wave","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"1,18,18,47\"}]"} {"title":"Intensity of the sound","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"228,3,242,25\"}]"} {"title":"Reference intensity","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"203,40,230,57\"}]"}

Question

$\textbf{Intensity}$ of the sound

{"title":"Sound intensity level of a sound wave","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"1,18,18,47\"}]"} {"title":"Intensity of the sound","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"228,3,242,25\"}]"} {"title":"Reference intensity","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"203,40,230,57\"}]"}

Question

$\textbf{Sound intensity level}$ of a sound wave

{"title":"Sound intensity level of a sound wave","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"1,18,18,47\"}]"} {"title":"Intensity of the sound","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"228,3,242,25\"}]"} {"title":"Reference intensity","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"203,40,230,57\"}]"}

Review

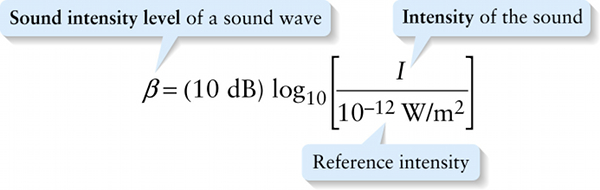
Let’s now see how the logarithm is used for describing the intensity of a sound. The argument of the logarithm must be a pure number without dimensions or units. We satisfy this requirement by taking the ration of the intensity $I$ of a sound to $10^{-12}\mathrm{W/m^2}$ , the intensity of a 1000-Hz tone at the threshold of hearing. The $\textbf{sound intensity level}$ of a sound with intensity $I$ equals the base-10 logarithm of this ratio multiplied by 10: