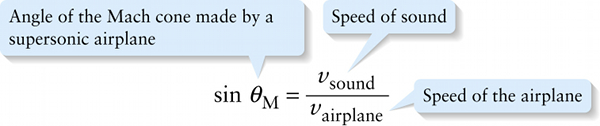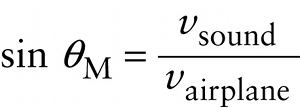Mach angle (13-37)

Review

The angle of the Mach cone depends on the airplane’s speed, which we call $v_{\mathrm{airplane}}$. To see how to calculate this angle, inspect parts (a) and (b) of Figure 13-27. In a time $\Delta{t}$ the airplane travels a distance $v_{\mathrm{airplane}}\Delta{t}$; this is shown by a blue line in Figure 13-27a and Figure 13-27b. The distance $v_{\mathrm{airplane}}\Delta{t}$ forms the hypotenuse of a right triangle, one leg of which is the distance $v_{\mathrm{sound}}\Delta{t}$ that the sound travels in time $\Delta{t}$. The sine of the angle $\theta_{\mathrm{M}}$ in Figure 13-27b, known as the $\textbf{Mach angle}$, equals the side opposite this angle ($v_{\mathrm{sound}}\Delta{t}$) divided by the hypotenuse ($v_{\mathrm{airplane}}\Delta{t}$). The factors of $\Delta{t}$ cancel, leaving