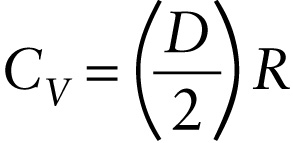Molar specific heat at constant volume for an ideal gas (15-18)

Question 1 of 3

Question

Number of degrees of freedom for a molecule of the gas

{"title":"Molar specific heat of an ideal gas at constant volume","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"rect\",\"coords\":\"3,44,44,90\"},{\"shape\":\"poly\",\"coords\":\"144,22\"}]"} {"title":"Number of degrees of freedom for a molecule of the gas","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"165,9,210,55\"}]"} {"title":"Ideal gas constant","description":"Wrong","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"249,40,290,93\"}]"}

Review

We'll use the symbol $D$ to represent the number of degress of freedom. Then the average energy per gas molecule is $(D/2)kT$ . One mole of the gas contains Avogadro's number of molecules, so the energy per mole is $N_A(D/2)kT = (D/2)\ (N_Ak)T = (D/2)RT$ . (Again, recall that $k = R/N_A$ , so $R = N_Ak)$ .) Then the internal energy of $n$ moles of ideal gas is

(15-16) $U = n\left(\frac{D}{2}R\right)T$ (ideal gas, $D$ degrees of freedom)

If the temperature of the gas changes by $\Delta{T}$ , it follows from Equation 15-16 that the internal energy change is

(15-17) $\Delta{U} = n\left(\frac{D}{2}R\right)\Delta{T}$ (ideal gas, $D$ degrees of freedom)

But, we saw above that for an ideal gas, $\Delta{U} = nC_V\ \Delta{T}$ . Comparing this to Equation 15-17, we see that