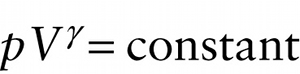Pressure and volume for ideal gas, adiabatic process (15-22)

Question 1 of 4

Question

Ratio of specific heats of the gas = $C_p / C_V$

{"title":"Pressure of an ideal gas","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"1,29,24,73\"}]"} {"title":"Volume of an ideal gas","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"28,18,65,65\"}]"} {"title":"Ratio of specific heats of the gas = C sub p /C sub V","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"66,19,90,53\"}]"} {"title":"The quantity pVγ has the same value at all times during an adiabatic process for an ideal gas.","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"125,33,301,70\"}]"}

Question

The quantity $pV^\gamma$ has the same value at all times during an adiabatic process for an ideal gas.

{"title":"Pressure of an ideal gas","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"1,29,24,73\"}]"} {"title":"Volume of an ideal gas","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"28,18,65,65\"}]"} {"title":"Ratio of specific heats of the gas = C sub p /C sub V","description":"Wrong","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"66,19,90,53\"}]"} {"title":"The quantity pVγ has the same value at all times during an adiabatic process for an ideal gas.","description":"Correct!","type":"correct","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"125,33,301,70\"}]"}

Review

The ratio of specific heats $\gamma = C_p\ /\ C_V$ for an ideal gas plays an important role in adiabatic processes in which there is zero heat flow into or out of the gas. If we have a quantity of gas in a cylinder with a moveable piston and then allow the piston to move in or out, the gas will compress or expand adiabatically if the cylinder and piston are made of an insulating material that does not allow heat to flow through it. It can be shown that if an ideal gas expands or contracts adiabatically, the pressure $p$ and volume $V$ of the gas are related by