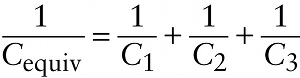Equivalent capacitance of capacitors in series (17-22)

Question 1 of 2

Question

Capacitances of the individual capacitors

{"title":"Equivalent capacitance of capacitors in series","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"3,41,24,67\"}]"} {"title":"Capacitances of the individual capacitors","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"119,43,148,68\"},{\"shape\":\"rect\",\"coords\":\"191,42,220,68\"},{\"shape\":\"rect\",\"coords\":\"262,41,288,68\"}]"}

Review

For the equivalent capacitor alone, of capacitance $C_{\mathrm{equiv}}$ , Equation 17-14 says that $q=C_{\mathrm{equiv}}V$ or $V = q/C_{\mathrm{equiv}}$ . If we compare this to Equation 17-21, we see that

If there are more than three capacitors in series, the same rule given in Equation 17-22 applies.