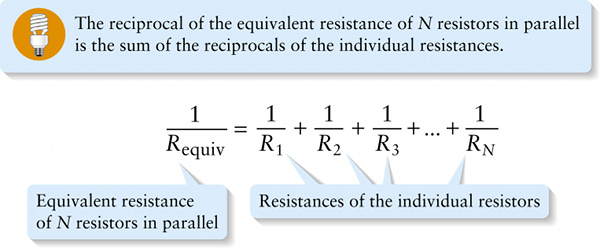
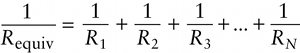Equivalent resistance of resistors in parallel (18-20)

Question 1 of 2

Question

Equivalent resistance of $N$ resistors in parallel

{"title":"Equivalent resistance of N resistors in parallel","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"1,29,16,46\"}]"} {"title":"Resistances of the individual resistors","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"136,26,154,49\"},{\"shape\":\"rect\",\"coords\":\"190,28,206,50\"},{\"shape\":\"rect\",\"coords\":\"83,28,101,47\"},{\"shape\":\"rect\",\"coords\":\"273,26,288,48\"}]"}

Review

Equation 18-20 tells us that by combining resistors in parallel, we create a circuit with a smaller equivalent resistance than any of the individual resistors. For the special case of two identical resistors $R$ in parallel, the equivalent resistance is given by

$\frac{1}{R_{\mathrm{equiv}}} = \frac{1}{R} + \frac{1}{R} = \frac{2}{R}$ so $R_{\mathrm{equiv}} = \frac{R}{2}$

The equivalent resistance of two identical resistors in parallel is onehalf that of each individual resistor.