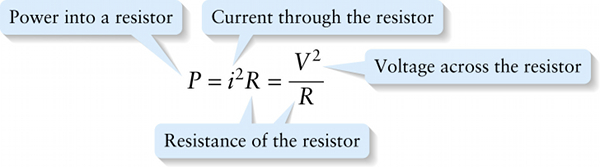
Power for a resistor (18-24)

Question 1 of 4

Question

Resistance of the resistor

{"title":"Power into a resistor","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"2,63,33,111\"}]"} {"title":"Current through the resistor","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"87,67,107,110\"}]"} {"title":"Voltage across the resistor","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"233,24,273,70\"}]"} {"title":"Resistance of the resistor","description":"Correct!","type":"correct","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"128,63,162,108\"},{\"shape\":\"rect\",\"coords\":\"243,101,284,141\"}]"}

Review

Figure 21-2 graphs the voltage $V(t)$ as a function of time. The angular frequency $\omega$ of the voltage (in rad/s) is related to the frequency $f$ of the voltage (in Hz) by the same relationship we used in Section 12-3 for simple harmonic motion:

$\omega = 2\pi{f}$

The period $T$ of the oscillation is equal to $1/f$ . For example, in the United States and Canada ac voltage is applied at a frequency $f = 60\ \mathrm{Hz}$ , so the period of oscillation is $T = 1/f = 1/ (60\ \mathrm{Hz})= 0.017 \mathrm{s}$ and the angular frequency is $\omega = 2\pi{f} = (2\pi\mathrm{rad})\ (60\ \mathrm{Hz}) = 3.8 \times 10^2\ \mathrm{rad}/s$ .

If we attach a source of ac voltage described by Equation 21-1 to a resistor of resistance $R$ , we can still use Equation 18-24 to calculate the power that flows into the resistor: