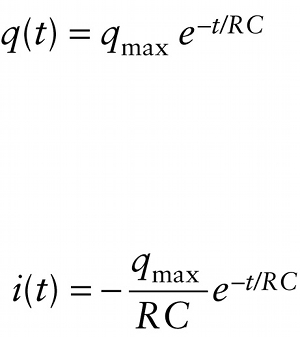Capacitor charge and current in a discharging series RC circuit (18-30)

Question 1 of 4

Question

Capacitor charge at $t = 0$

{"title":"Capacitor charge as a function of time","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"35,19,45,51\"}]"} {"title":"The product RC (resistance multiplied by capacitance) is the time constant of the circuit.","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"228,14,265,37\"},{\"shape\":\"rect\",\"coords\":\"263,267,299,293\"},{\"shape\":\"rect\",\"coords\":\"135,300,194,333\"}]"} {"title":"Current as a function of time","description":"Wrong","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"35,274,48,303\"}]"} {"title":"Capacitor charge at t = 0","description":"Correct!","type":"correct","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"131,251,155,284\"},{\"shape\":\"rect\",\"coords\":\"98,26,122,53\"}]"}

Question

The product $RC$ (resistance multiplied by capacitance) is the time constant of the circuit.

{"title":"Capacitor charge as a function of time","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"35,19,45,51\"}]"} {"title":"The product RC (resistance multiplied by capacitance) is the time constant of the circuit.","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"228,14,265,37\"},{\"shape\":\"rect\",\"coords\":\"263,267,299,293\"},{\"shape\":\"rect\",\"coords\":\"135,300,194,333\"}]"} {"title":"Current as a function of time","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"35,274,48,303\"}]"} {"title":"Capacitor charge at t = 0","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"131,251,155,284\"},{\"shape\":\"rect\",\"coords\":\"98,26,122,53\"}]"}

Review

The graphs in Figure 18-20 show the charge $q$ and current $i$ as given by Equations 18-30. Both functions are proportional to $e^{-t/RC}$ , so both decrease by a factor of $1/e$ whenever time $t$ increases by one time constant $RC$ . So the value of $RC$ determines both how rapidly the capacitor charges and how rapidly it discharges.