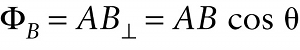Magnetic flux (20-1)

Question 1 of 5

Question

Magnetic flux through a surface

{"title":"Magnetic flux through a surface","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"1,2,25,34\"}]"} {"title":"Area of the surface","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"77,5,100,32\"},{\"shape\":\"rect\",\"coords\":\"172,5,196,33\"}]"} {"title":"Angle between the magnetic field and the perpendicular to the surface","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"281,5,300,31\"}]"} {"title":"Magnitude of the magnetic field","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"199,5,218,32\"}]"} {"title":"The component of magnetic field perpendicular to the surface","description":"Incorrect","type":"incorrect","color":"#333333","code":"[{\"shape\":\"rect\",\"coords\":\"101,5,122,32\"}]"}

Review

It turns out that a simple way to describe the emf in any of these situations is in terms of the change in magnetic flux through the loop in Figures 20-2 and 20-3. We define this in the same way that we defined electric flux in Section 16-6: It’s the area $A$ of the surface outlined by the loop, multiplied by $B \cos{\theta}$ , the component of the magnetic field that’s perpendicular to that surface (see part (a) of Figure 20-4). In equation form, the magnetic flux $\Phi_B$ (“phi-sub-B”) through the loop is

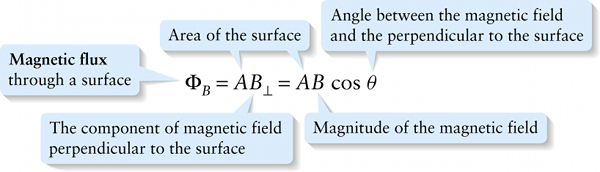
(The subscript $B$ reminds us that this is the flux of the magnetic field $\vec{B}$ .) As parts (b) and (c) of Figure 20-4 show, the flux $\Phi_B$ can be positive or negative.