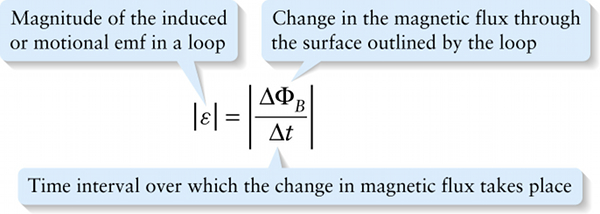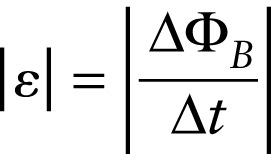Processing math: 100%

Faraday’s law of induction (20-2)

Balloon Art Concept Check: Click on the part of the equation that is described by the bubble text shown

Question 1 of 3

Question

Time interval over which the change in magnetic flux takes place
Feedback
{"title":"Magnitude of the induced or motional emf in a loop","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"14,66,43,102\"}]"} {"title":"Change in the magnetic flux through the surface outlined by the loop","description":"Incorrect","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"183,6,232,53\"}]"} {"title":"Time interval over which the change in magnetic flux takes place","description":"Correct!","type":"correct","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"205,97,233,136\"}]"}

Review

This law states that the magnitude of the emf that appears in a loop is equal to the magnitude of the rate of change of the magnetic flux through the loop. If a large change in flux ΔΦB happens in a short time interval Δt, the resulting emf has a large magnitude; if the change in flux is relatively small and happens over a long time interval, the resulting emf has a small magnitude.

Note that Equation 20-2 tells us only the magnitude of the emf, not its direction. In the following section we’ll see how the direction is determined.