Magnetic and electric energies in an LC circuit (21-27)
Question
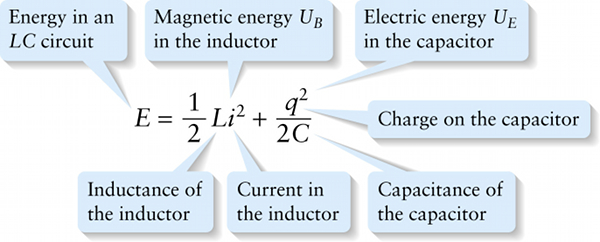
Energy in an LC circuit
{"title":"Energy in an LC circuit","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"1,46,30,86\"}]"} {"title":"Current in the inductor","description":"Incorrect","type":"incorrect","color":"#008000","code":"[{\"shape\":\"rect\",\"coords\":\"157,50,172,88\"}]"} {"title":"Inductance of the inductor","description":"Incorrect","type":"incorrect","color":"#FF6600","code":"[{\"shape\":\"rect\",\"coords\":\"131,49,157,87\"}]"} {"title":"Magnetic energy U sub B in the inductor","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"125,33,188,99\"}]"} {"title":"Electric energy U sub E in the capacitor","description":"Incorrect","type":"incorrect","color":"#333300","code":"[{\"shape\":\"rect\",\"coords\":\"279,12,294,38\"}]"} {"title":"Charge on the capacitor","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"256,30,280,67\"}]"} {"title":"Capacitance of the capacitor","description":"Incorrect","type":"incorrect","color":"#ff0000","code":"[{\"shape\":\"rect\",\"coords\":\"268,76,298,112\"}]"}Review
We recognize the second term on the right-hand side of Equation 21-27,q2/2C, from Section 17-6: It’s just the electric potential energy stored in the capacitor. Since a capacitor plays the same role in an LC circuit as the spring does in a block–spring combination, this electric potential energy is analogous to the elastic potential energy of a spring. We use the symbol UE for this electric energy. The subscript E reminds us that an →E-field is involved; you can think of UEas the energy required to take an uncharged capacitor and move charges +q and −q to the plates of the capacitor, thereby setting up an electric field →E between the plates.
The first term on the right-hand side of Equation 21-27, (1/2)Li2, is one that we haven’t seen before. The presence of the inductance L in this term tells us that it represents energy stored in the inductor as a result of the presence of current. To see how this energy arises, recall from Section 21-4 that an inductor sets up an emf that opposes any change in the current through the inductor. If we want to make current flow through an inductor where none was flowing before, we have to do work against that emf. The quantity (1/2)Li2 is exactly equal to the amount of work we have to do. By building up the current from zero to i, we also create a magnetic field →B, so we can think of (1/2)Li2 as the energy required to set up a magnetic field in and around the inductor. That’s why we call this magnetic energy and denote it by the symbol UB (the subscrip B reminds us that a →B-field is involved).