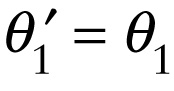The law of reflection (23-1)
Question
When light reflects at the boundary between two media, the angle of the reflected ray from the normal...
{"title":"When light reflects at the boundary between two media, the angle of the reflected ray from the normal...","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"3,8,40,54\"}]"} {"title":"...is equal to the angle of the incident ray from the normal.","description":"Incorrect","type":"incorrect","color":"#008000","code":"[{\"shape\":\"rect\",\"coords\":\"123,7,156,56\"}]"}Review
The line BB′ in Figure 23-4a is perpendicular to the incident wave front and so points in the direction of the incident ray. Likewise, the line AA′ is perpendicular to the reflected wave front and so points in the direction of the reflected ray. We can determine how these directions are related to each other by noticing that the triangles ABB′ and AA′B′ are both right triangles, both have the same hypotenuse of length AB′, and both have one side of length v1Δt (Figure 23-4b). You can see that these two right triangles are identical, except that triangle AA′B′has been flipped left-to-right compared to triangle ABB9. So the angle θ′1 of the line AA′ measured from the vertical (that is, from the normal to the boundary) must be the same as the angle θ1 of the line BB′ measured from the vertical. We conclude that