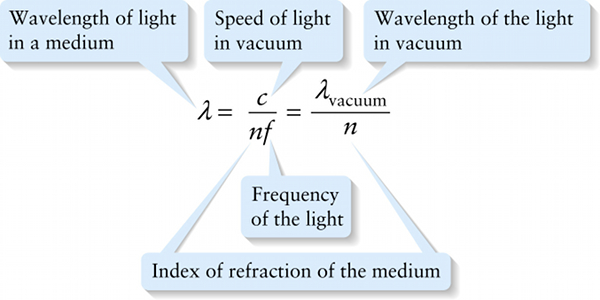
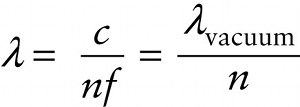Wavelength of light in a medium (23-8)

Question 1 of 5

Question

Index of refraction of the medium

{"title":"Wavelength of light in a medium","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"1,34,26,68\"}]"} {"title":"Speed of light in vacuum","description":"Incorrect","type":"incorrect","color":"#008000","code":"[{\"shape\":\"rect\",\"coords\":\"90,22,115,48\"}]"} {"title":"Wavelength of the light in vacuum","description":"Wrong","type":"incorrect","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"185,3,209,37\"}]"} {"title":"Index of refraction of the medium","description":"Correct!","type":"correct","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"82,76,104,102\"},{\"shape\":\"rect\",\"coords\":\"223,66,255,94\"}]"} {"title":"Frequency of the light","description":"Incorrect","type":"incorrect","color":"#ff0000","code":"[{\"shape\":\"rect\",\"coords\":\"103,65,123,108\"}]"}

Review

Equation 23-8 says that the wavelength is shorter in a medium with a higher index of refraction, where the propagation speed is slower. For example, red light that has a wavelength $\lambda_{\mathrm{vacuum}} = 750$ nm in vacuum has a wavelength in water ( $n$ = 1.33) equal to $\lambda = \lambda_{\mathrm{vacuum}} / n = (750 \mathrm{nm}) / (1.33) = 564$ nm. The frequency of this light is the same in both media: $f = c / \lambda_{\mathrm{vacuum}} = (3.00 \times 10^8 \mathrm{m}/\mathrm{s}) / (750 \times 10^{-9} \mathrm{m}) = 4.00 \times 10^{14}$ Hz in vacuum and $f = v/\lambda = c / (n\lambda) = (3.00 \times 10^8 \mathrm{m}/\mathrm{s}) / ((1.33)(564 \times 10^{-9} \mathrm{m}))= 4.00 \times 10^{14}$ Hz in water.