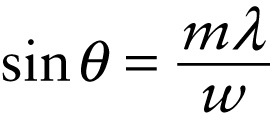Dark fringes in diffraction through a slit (23-24)

Balloon Art Concept Check: Click on the part of the equation that is described by the bubble text shown

Question 1 of 4

Question

Wavelength of the light in vacuum
Feedback
{"title":"Angle between the normal to the slit and the location of the mth dark fringe","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"78,39,114,84\"}]"} {"title":"Number of the dark fringe: m = 1, 2, 3, ...","description":"Wrong","type":"incorrect","color":"#008000","code":"[{\"shape\":\"rect\",\"coords\":\"182,19,232,53\"}]"} {"title":"Wavelength of the light in vacuum","description":"Correct!","type":"correct","color":"#ffcc00","code":"[{\"shape\":\"rect\",\"coords\":\"232,3,267,53\"}]"} {"title":"Width of the slit","description":"Incorrect","type":"incorrect","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"198,77,250,118\"}]"}

Review

In general, the angle of the \(m^{\mathrm{th}}\) dark fringe is given by

Equations 23-22 and 23-23 are special cases of Equation 23-24, with \(m = 1\) and \(m = 2\) respectively.