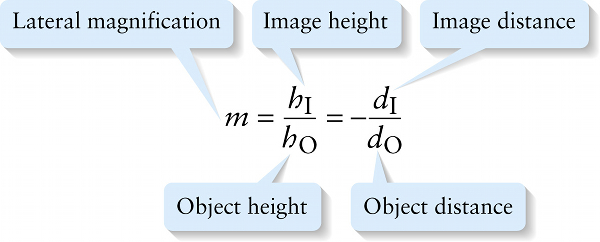
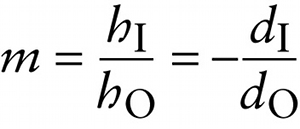Chapter 24. Lateral magnification for a mirror or lens (24-14)

Review

A negative value of the magnification m means that the image is inverted, as in Figure 24-18. If m is positive, the image is upright. (As we’ll see in Section 24-8, the same equation also applies to lenses.)

We’ve derived Equation 24-14 for the case in which the image is in front of the mirror (the same side as the object) and hence real, but it’s also true when the image is on the back side of the mirror and hence virtual. When the object is far from the mirror and the image is close to the focal point, \(d_{\mathrm{I}}\) is positive and small compared to \(d_{\mathrm{O)}}\), so \(m\) is small and negative; the mirror produces a reduced, inverted image (see Figure 24-12). As the object distance decreases, the image distance increases and the ratio \(m = d_{\mathrm{I}} / d_{\mathrm{O}}\) increases in absolute value. As we saw above, when \(d_{\mathrm{O}} = 2f\) the image distance \(d_{\mathrm{I}}\) is also equal to \(2f\); then \(m = -1\) and the inverted image is as large as the object (see Figure 24-13). If we move the object even closer to the focal point, but still outside it, the image distance is greater than the object distance and the absolute value of the magnification is greater than 1. Hence the inverted image is larger than the object (see Figure 24-14). If we move the object inside the focal point so that \(d_{\mathrm{O}} > f\), the image distance is negative (the image is behind the mirror) and the image is virtual. In this case Equation 24-14 tells us that \(m\) is positive, so the virtual image is upright (see Figure 24-16). We see that Equation 24-14 gives us the same results as we deduced from the ray diagrams in Section 24-3. Table 24-1 summarizes when the radius of curvature