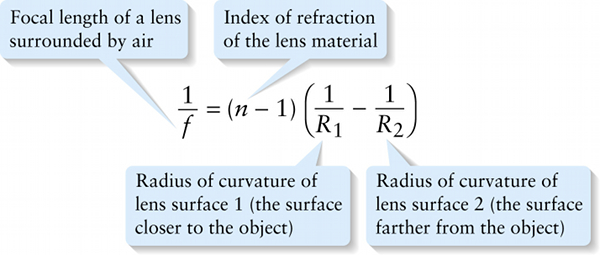
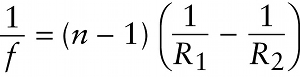Lensmaker’s equation for the focal length of a thin lens (24-24)
Question 1 of 4
Question
Radius of curvature of lens surface 1 (the surface closer to the object)
{"title":"Focal length of a lens surrounded by air","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"4,40,20,75\"}]"} {"title":"Index of refraction of the lens material","description":"Incorrect","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"70,26,89,48\"}]"} {"title":"Radius of curvature of lens surface 2 (the surface farther from the object)","description":"Wrong","type":"incorrect","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"249,39,271,68\"}]"} {"title":"Radius of curvature of lens surface 1 (the surface closer to the object)","description":"Correct!","type":"correct","color":"#000080","code":"[{\"shape\":\"rect\",\"coords\":\"172,40,194,69\"}]"}Review
Equation 24-24 can be derived by applying Snell’s law of refraction (Equation 23-6) to a ray of light refracted by both surfaces of a lens. The derivation is beyond our scope, however.
The values of the radii of curvature R1 and R2 depend on how sharply and in what direction the two surfaces of the lens are curved. As Figure 24-34 shows, we take a radius to be positive if the center of curvature is on the other side of the lens from the object, but negative if the center of curvature is on the same side as the object. For example, in Figure 24-34 the radius R1 of surface 1 is positive, but the radius R1 of surface 2 is negative.