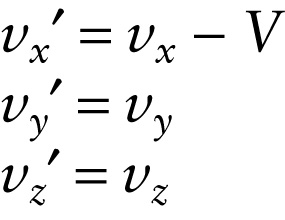Galilean velocity transformation (25-5)

Question 1 of 3

Question

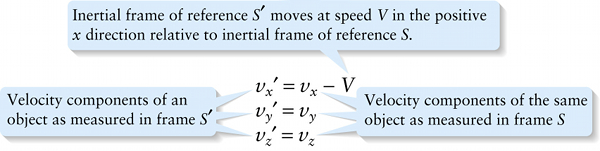
Velocity components of an object as measured in frame $S′$

{"title":"Inertial frame of reference S′ moves at speed V in the positive x direction relative to inertial frame of reference S.","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"243,4,285,57\"}]"} {"title":"Velocity components of the same object as measured in frame S","description":"Wrong","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"127,21,157,56\"},{\"shape\":\"rect\",\"coords\":\"123,88,155,125\"},{\"shape\":\"rect\",\"coords\":\"120,158,152,199\"}]"} {"title":"Velocity components of an object as measured in frame S′","description":"Correct!","type":"correct","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"1,22,34,56\"},{\"shape\":\"rect\",\"coords\":\"1,92,33,126\"},{\"shape\":\"rect\",\"coords\":\"2,158,28,197\"}]"}

Question

Velocity components of the same object as measured in frame $S$

{"title":"Inertial frame of reference S′ moves at speed V in the positive x direction relative to inertial frame of reference S.","description":"Incorrect","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"243,4,285,57\"}]"} {"title":"Velocity components of the same object as measured in frame S","description":"Correct!","type":"correct","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"127,21,157,56\"},{\"shape\":\"rect\",\"coords\":\"123,88,155,125\"},{\"shape\":\"rect\",\"coords\":\"120,158,152,199\"}]"} {"title":"Velocity components of an object as measured in frame S′","description":"Incorrect","type":"incorrect","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"1,22,34,56\"},{\"shape\":\"rect\",\"coords\":\"1,92,33,126\"},{\"shape\":\"rect\",\"coords\":\"2,158,28,197\"}]"}

Question

Inertial frame of reference $S'$ moves at speed $V$ in the positive $x$ direction relative to inertial frame of reference $S$ .

{"title":"Inertial frame of reference S′ moves at speed V in the positive x direction relative to inertial frame of reference S.","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"243,4,285,57\"}]"} {"title":"Velocity components of the same object as measured in frame S","description":"Incorrect","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"127,21,157,56\"},{\"shape\":\"rect\",\"coords\":\"123,88,155,125\"},{\"shape\":\"rect\",\"coords\":\"120,158,152,199\"}]"} {"title":"Velocity components of an object as measured in frame S′","description":"Incorrect","type":"incorrect","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"1,22,34,56\"},{\"shape\":\"rect\",\"coords\":\"1,92,33,126\"},{\"shape\":\"rect\",\"coords\":\"2,158,28,197\"}]"}

Review

Equations 25-5, which relate the velocity of an object in frame $S'$ to the velocity of the same object in frame $S$ , are called the Galilean velocity transformation.

As an example, think again of the ball shown in Figure 25-5. If the ball moves straight up and down as measured in frame $S'$ , then in that frame the ball is in free fall with only a $y$ component of velocity. The other two components The other two components are zero: $v_x' = v_z' = 0$ . As measured in frame $S$ , the velocity of the ball has component

$\begin{eqnarray*} v_x &=& v_x' + V = V \\ v_y &=& v_y'\\ v_z &=& v_z' = 0 \end{eqnarray*}$

As measured in frame $S$ , the ball moves up and down along the $y$ direction with the same velocity as measured in frame $S': v_y = v_y'$ . At the same time, as measured in frame $S$ the ball maintains a constant velocity $V$ in the $x$ direction. That’s just the behavior we expect for a projectile: Its motion is a combination of up-and-down free fall and constant-velocity horizontal motion (see Section 3-6).