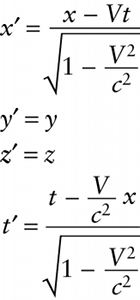Lorentz transformation (25-15)

Question 1 of 3

Question

Inertial frame of reference $S'$ moves at speed $V$ in the positive $x$ direction relative to inertial frame of reference $S$

{"title":"Inertial frame of reference S′ moves at speed V in the positive x direction relative to inertial frame of reference S.","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"104,1,122,23\"}]"} {"title":"Coordinates of the same event as measured in frame S","description":"Incorrect","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"121,4,134,24\"},{\"shape\":\"rect\",\"coords\":\"41,113,60,133\"},{\"shape\":\"rect\",\"coords\":\"41,148,59,166\"},{\"shape\":\"rect\",\"coords\":\"118,190,139,207\"}]"} {"title":"Coordinates of an event as measured in frame S′","description":"Incorrect","type":"incorrect","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"1,22,14,37\"},{\"shape\":\"rect\",\"coords\":\"1,112,13,135\"},{\"shape\":\"rect\",\"coords\":\"1,147,16,167\"},{\"shape\":\"rect\",\"coords\":\"2,218,12,237\"}]"}

Question

Coordinates of the same event as measured in frame $S$

{"title":"Inertial frame of reference S′ moves at speed V in the positive x direction relative to inertial frame of reference S.","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"104,1,122,23\"}]"} {"title":"Coordinates of the same event as measured in frame S","description":"Correct!","type":"correct","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"121,4,134,24\"},{\"shape\":\"rect\",\"coords\":\"41,113,60,133\"},{\"shape\":\"rect\",\"coords\":\"41,148,59,166\"},{\"shape\":\"rect\",\"coords\":\"118,190,139,207\"}]"} {"title":"Coordinates of an event as measured in frame S′","description":"Incorrect","type":"incorrect","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"1,22,14,37\"},{\"shape\":\"rect\",\"coords\":\"1,112,13,135\"},{\"shape\":\"rect\",\"coords\":\"1,147,16,167\"},{\"shape\":\"rect\",\"coords\":\"2,218,12,237\"}]"}

Question

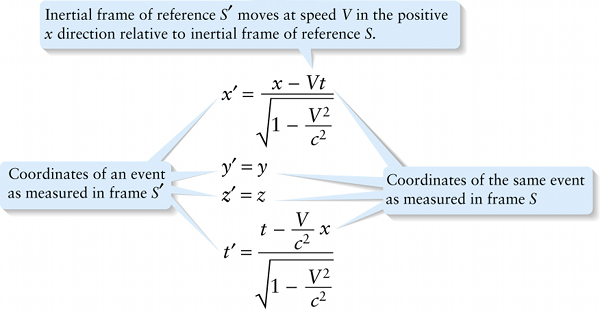
Coordinates of an event as measured in frame $S′$

{"title":"Inertial frame of reference S′ moves at speed V in the positive x direction relative to inertial frame of reference S.","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"104,1,122,23\"}]"} {"title":"Coordinates of the same event as measured in frame S","description":"Incorrect","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"121,4,134,24\"},{\"shape\":\"rect\",\"coords\":\"41,113,60,133\"},{\"shape\":\"rect\",\"coords\":\"41,148,59,166\"},{\"shape\":\"rect\",\"coords\":\"118,190,139,207\"}]"} {"title":"Coordinates of an event as measured in frame S′","description":"Correct!","type":"correct","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"1,22,14,37\"},{\"shape\":\"rect\",\"coords\":\"1,112,13,135\"},{\"shape\":\"rect\",\"coords\":\"1,147,16,167\"},{\"shape\":\"rect\",\"coords\":\"2,218,12,237\"}]"}

Review

The Galilean transformation that we presented in Section 25-2 is not consistent with the postulates of special relativity. A set of transformation equations that is consistent with relativity is the Lorentz transformation. As in Figure 25-3, we take frame $S'$ to be moving at speed $V$ in the positive $x$ direction relative to frame $S$ . The origins of the two frames coincide at $t = 0$ in frame $S$ and $t' = 0$ in frame $S'$ . If an event takes place at coordinates $x, y, z, t$ in frame $S$ , the coordinates of that same event in frame $S'$ are