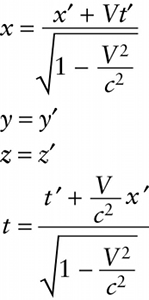Inverse Lorentz transformation (25-16)
Question 1 of 3
Question
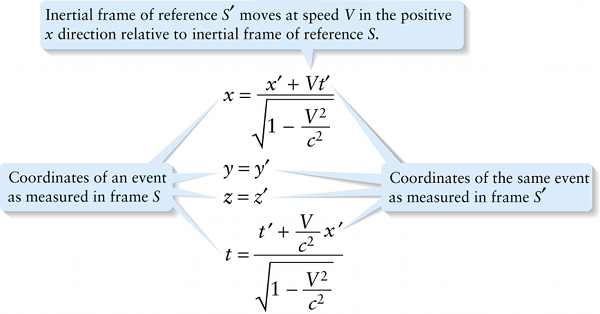
Inertial frame of reference S′ moves at speed Vin the positive x direction relative to inertial frame of reference S.
{"title":"Inertial frame of reference S′ moves at speed V in the positive x direction relative to inertial frame of reference S.","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"103,1,119,23\"}]"} {"title":"Coordinates of the same event as measured in frame S'","description":"Incorrect","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"38,113,57,133\"},{\"shape\":\"rect\",\"coords\":\"37,146,55,164\"},{\"shape\":\"rect\",\"coords\":\"124,189,142,206\"},{\"shape\":\"rect\",\"coords\":\"118,7,128,25\"}]"} {"title":"Coordinates of an event as measured in frame S","description":"Incorrect","type":"incorrect","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"1,22,14,37\"},{\"shape\":\"rect\",\"coords\":\"1,112,13,135\"},{\"shape\":\"rect\",\"coords\":\"1,147,16,167\"},{\"shape\":\"rect\",\"coords\":\"2,218,12,237\"}]"}Review
Equations 25-15 are useful for finding the coordinates of an event in frame S′ if we know the event’s coordinates in frame S. If we instead want to determine the coordinates of an event in frame S from the coordinates in frame S′, it’s most convenient to use the inverse Lorentz transformation: