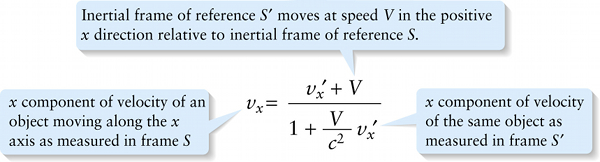
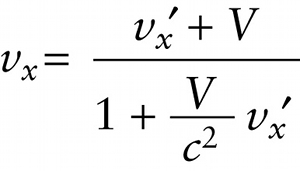Inverse Lorentz velocity transformation (25-18)
Question 1 of 3
Question
Inertial frame of reference S′ moves at speed V in the positive x direction relative to inertial frame of reference S.
{"title":"Inertial frame of reference S′ moves at speed V in the positive x direction relative to inertial frame of reference S.","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"224,3,259,44\"}]"} {"title":"x component of velocity of the same object as measured in frame S′","description":"Incorrect","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"246,106,269,132\"}]"} {"title":"x component of velocity of an object moving along the x axis as measured in frame S","description":"Incorrect","type":"incorrect","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"1,48,24,72\"}]"}Review
Equation 25-17 allows us to find the object’s velocity relative to frame S′ if we know its velocity relative to frame S. If instead we know the object’s velocity relative to frame S′ and want to calculate its velocity relative to frame S, we use the inverse Lorentz velocity transformation: