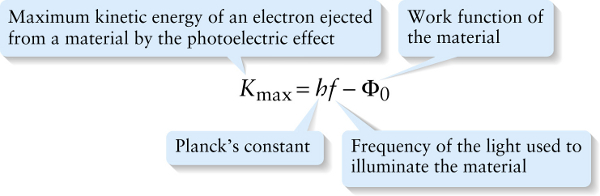
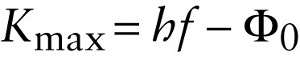Maximum kinetic energy of an electron in the photoelectric effect (26-1)

Question 1 of 4

Question

Frequency of the light used to illuminate the material

{"title":"Maximum kinetic energy of an electron ejected from a material by the photoelectric effect","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"1,2,35,45\"}]"} {"title":"Work function of the material","description":"Incorrect","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"244,6,279,47\"}]"} {"title":"Frequency of the light used to illuminate the material","description":"Correct!","type":"correct","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"177,2,201,56\"}]"} {"title":"Planck’s constant","description":"Incorrect","type":"incorrect","color":"#ff0000","code":"[{\"shape\":\"rect\",\"coords\":\"149,4,177,51\"}]"}

Review

Equation 26-1 tells us that that a graph of $K_{\mathrm{max}}$ as a function of the light frequency $f$ should be a straight line of slope $h$ (see Figure 26-3). Since kinetic energy can never be negative, Equation 26-1 also tells us that electrons will be emitted only if $hf - \Phi_0 > 0$ .