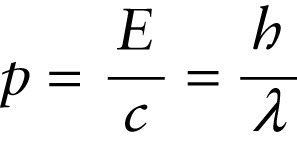Momentum and energy of a photon (26-7)

Question 1 of 5

Question

Wavelength of the photon

{"title":"Magnitude of the momentum of a photon","description":"Wrong","type":"incorrect","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"1,61,31,110\"}]"} {"title":"Energy of the photon","description":"Incorrect","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"117,6,156,53\"}]"} {"title":"Planck’s constant","description":"Wrong","type":"incorrect","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"251,3,283,51\"}]"} {"title":"Wavelength of the photon","description":"Correct!","type":"correct","color":"#ff0000","code":"[{\"shape\":\"rect\",\"coords\":\"246,87,294,139\"}]"} {"title":"Speed of light in a vacuum","description":"Incorrect","type":"incorrect","color":"#800080","code":"[{\"shape\":\"rect\",\"coords\":\"120,102,153,137\"}]"}

Review

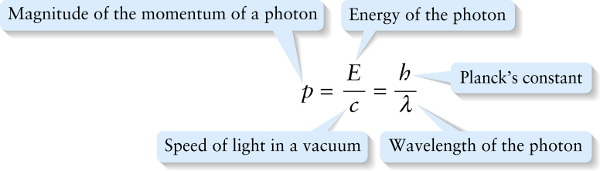
A photon has zero mass, which is why it can travel at the speed of light. (Any object with nonzero mass would require an infinite amount of kinetic energy to reach $v = c$ , as we described in Section 25-7.) As such, we can’t apply Equation 26-3 or 26-4 directly to photons. But we can use the combination in Equation 26-5, in which mass does not appear explicitly. Setting $v = c$ in Equation 26-5, we get the following relationship for the momentum of a photon:

(26-6) $p = \frac{E_c}{c^2} = \frac{E}{c}$ (momentum of a photon)

From Equation 22-26 we can write $E = hf$ , and we know that for light waves $c = f \lambda$ (Equation 22-2). If we substitute these into Equation 26-6, we get an alternative expression for the momentum of a photon:

$p = \frac{hf}{f\lambda}$

or, simplifying,