Heisenberg uncertainty principle (28-7)
Question
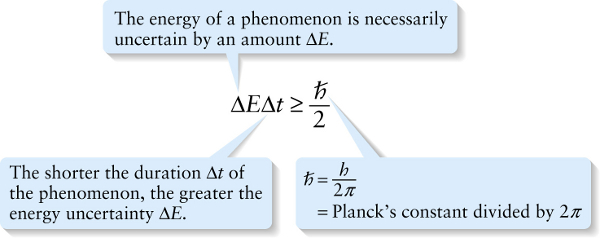
The energy of a phenomenon is necessarily uncertain by an amount ΔE.
{"title":"The energy of a phenomenon is necessarily uncertain by an amount ΔE.","description":"Correct!","type":"correct","color":"#99CCFF","code":"[{\"shape\":\"poly\",\"coords\":\"82,133\"},{\"shape\":\"rect\",\"coords\":\"10,16,12,16\"},{\"shape\":\"poly\",\"coords\":\"144,22\"},{\"shape\":\"rect\",\"coords\":\"35,35,76,85\"}]"} {"title":"hbar = h over 2 pi = Planck’s constant divided by 2 pi","description":"Incorrect","type":"incorrect","color":"#ffff00","code":"[{\"shape\":\"rect\",\"coords\":\"198,2,240,51\"}]"} {"title":"The shorter the duration Δt of the phenomenon, the greater the energy uncertainty ΔE.","description":"Incorrect","type":"incorrect","color":"#00ff00","code":"[{\"shape\":\"rect\",\"coords\":\"107,45,135,84\"}]"}Review
Another way to interpret Equation 28-7 is to say that it places limits on how precisely the law of conservation of energy must be obeyed. Suppose a system undergoes some kind of process that lasts for a time Δt. Equation 28-7 says that the energy of the system is necessarily uncertain during that process, and the minimum energy uncertainty is given by ΔEΔt=ℏ/2 or ΔE=ℏ/(2Δt). So it’s fundamentally impossible to measure the energy of the system with an uncertainty less than ℏ/(2Δt). This means that during the process, the energy of the system could actually vary by as much as ℏ/(2Δt), and there would be no way that we could tell that the energy had changed value—that is, that the energy was not conserved. The shorter the duration Δt of the process, the greater the amount ℏ/(2Δt)by which energy conservation can be (temporarily) violated during that time Δt. Stated another way, it’s acceptable to violate the law of conservation of energy by an amount ΔE, provided the duration of time during which the law is violated is no more than Δt=ℏ/(2ΔE).