CHAPTER 9 APPENDIXBond Pricing and Arbitrage
Bond pricing may seem complicated but it can be understood with a few simple principles. Let’s start with something more familiar than bonds. Suppose that you invest $100 in a savings account that pays a 10% rate of interest. How much money will you have in one year? That’s easy; every dollar invested at 10% turns into $1.10 in one year so $100 invested at 10% turns into $110, which we can write as $100 × (1.10) = $110.
More generally, let’s call the money that you invest the present value (PV), let’s call the interest rate r, and let’s call the money that you will withdraw from the bank in one year the future value (FV). Then, the relationship between PV, r, and FV is simply

For example, if you invested $100 in present value at an interest rate of 5%, how much money would you have in a year (FV)? Substituting in equation 1, we have $100 × (1.05) = $105.
Okay, now let’s ask a slightly more difficult question. Suppose that the interest rate is 10% and that in one year you would like to have the future value of $100. How much do you need to put in the bank today? In other words, if the interest rate is 10% and you want a future value of $100, what present value do you need to put in the bank? Let’s fill in what we know:

To solve for PV, divide both sides by 1.10:

Thus, if the interest rate is 10% and we want $100 in the bank in one year, we need to invest $90.91 today. More generally, we can rewrite equation 1 in any of the following three ways depending on whether we want to solve for FV, PV, or r:

We now have everything we need to explain bond pricing. Imagine that the interest rate is 10% and suppose that a bond exists that promises to pay $100 in one year’s time. Thus, the future value of the bond—conveniently this is also called the face value—is $100, the interest rate r is 10%, and we want to know PV. We can use version 1b of our equation:
203

In other words, when the interest rate is 10%, a bond promising to pay $100 in one year will sell for $90.91.
Students are often confused by the fact that interest rates and bond prices move in opposite directions: That is, when the interest rate rises, bond prices fall, and when the interest rate falls, bond prices rise. But now we can explain this result easily. We know that at an interest rate of 10% a bond that has a future value of $100 will have a price or present value of $90.91. So what happens to the present value of the same bond when the interest rate falls to 5%?

Substituting what we know, we have
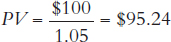
Thus, when the interest rate falls from 10% to 5%, the price of the bond rises from $90.91 to $95.23.
We can see from version 1b of our formula that the price of a bond rises when the interest rate falls (and vice versa), but what is the economics behind this result? To understand the economics, we will use version 1c of our equation.
Let’s suppose that the interest rate falls from 10% to 5%—in other words, the most that investors can earn on their loanable funds is a 5% rate of return. But imagine that instead of rising to $95.24, the price of a bond paying $100 in one year’s time stayed at $90.91. How much could investors earn by investing in this bond? The present value of the bond is $90.91, the future value is $100, so the return on this bond is

Now what would you do if every other investment in the economy is earning a 5% rate of return, but an equally safe bond exists that earns 10%? Correct, you would buy the bond paying 10%. And what happens when you—and everyone else—start buying this extraordinary bond? Correct, the bond increases in price and, as it increases in price, the return on the bond falls. In fact, the bond will increase in price and its rate of return will fall until it earns a rate of return roughly equal to that on similarly risky investments elsewhere in the economy.
Our last result can be stated more generally: Buying and selling will equalize the rate of return on equally risky assets. The buying and selling of equally risky assets is called “arbitrage.” Arbitrage is a very important idea with many more implications than we can address here, but if you continue on in economics or finance, you will study arbitrage in more detail.
204
We have shown how the simplest types of bonds are priced. Many bonds mature in more than one year and many bonds include coupon payments: periodic payments in addition to the final payment at maturity. The formula for determining the present value of a bond that matures in more than one year and that has coupon payments is more complicated than formula 1b, but the ideas are exactly the same. We will give one quick example to illustrate.
Let’s begin, once again, with a $100 investment in a savings account that pays a 10% rate of interest. But this time, let’s suppose that we invest the money for two years—what is the future value of this investment? We can break our two-year investment into two one-year investments. We first invest $100 at 10%, giving us $110 at the end of the first year. We then invest $110 at 10% for another year, which gives us $121 at the end of two years. In general terms, we can write

The term in the square brackets is how much we will have after the first year of investment; we then multiply this amount by (1 + r2), the rate of interest in year 2, to give us the amount that we will have at the end of two years.
As we did before, we can divide both sides of equation A1 by (1 + r1)(1 + r2) in order to rewrite A1 as

Let’s use formula A2 to figure out the present value or selling price of a bond that pays $100 in two years when the interest rate in year 1 and year 2 is 10%. Substituting what we know, we have

Thus, if the interest rate in year 1 and year 2 is 10%, then a bond that pays $100 two years from now has a present value or selling price of $82.64.
Now here is the big payoff. What is the price of a bond that pays $100 at the end of year 1 and another $100 at the end of year 2? We can easily price this bond because this bond is just a combination of two bonds, one of which pays $100 at the end of year 1 and one of which pays $100 at the end of year 2. But we just calculated the value of these bonds! And, because of arbitrage, the combination bond must sell for the same price as the sum of the two bonds that we calculated earlier, or $173.55 = $90.91 + $82.64.
We can also calculate the value of the combination bond directly. When the interest rate is 10%, the PV of a bond that pays $100 in one year and another $100 in two years is

205
Following through on the same logic, we can now calculate the price of very complicated bonds. The present value of a bond that makes potentially different payments every year for n years is

Bond Pricing with a Spreadsheet
We can calculate the price of bonds like this using a spreadsheet. Figure A9.1 shows a bond that pays $100 in each of the first nine years and then in the 10th year it pays $1,000. The present value of each payment is calculated in Column C. Note that the formula in cell C2,“=B2/(1+$D$2)^A2”, is equivalent to 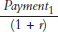 . Copying this formula for the nine other payments gives us a column of present values, which we sum up in cell C14,”=SUM(C2:C11)”, to find the price of the bond, $1,324.70.
. Copying this formula for the nine other payments gives us a column of present values, which we sum up in cell C14,”=SUM(C2:C11)”, to find the price of the bond, $1,324.70.
FIGURE A9.1

You can easily vary the interest rate to see what happens to the price of the bond. If the interest rate rises to 10%, for example, we have the result in Figure A9.2 on the next page.
206
FIGURE A9.2

And thus, the price of the bond falls to $961.45. Note once again that a higher interest rate means a lower price for the bond. It’s also interesting to see that a higher interest rate has a small effect on payments that come soon (compare the PV of the first payment in Figure A9.1 and Figure A9.2), but a very large effect on payments far into the future (compare the PV of the final payment in the two scenarios).
One final point of importance. Bond pricing might seem to be far away from your interests, but the techniques in this appendix can be used to price and understand any kind of asset that has a payment stream over time. A mortgage, for example, is very similar to a bond except instead of receiving bond payments, you will typically be sending mortgage payments. If you want to compare two different mortgages, for example, a 20-year mortgage and a 30-year mortgage where the mortgages have different interest rates, you will want to compute the present value of each mortgage to find the one with the lowest PV. Online mortgage calculators help you to do this. What those calculators do is compute present values using the same types of techniques as found in this appendix.
* In principle, it is possible for the supply curve for savings to be negatively sloped. For instance, if an individual wanted exactly $100 in one year’s time, then at an interest rate of 10%, he or she would need to save $90.91, but at an interest rate of 20%, he or she would need to save only $83.33. Thus, an increase in the interest rate could reduce savings. The evidence, however, indicates that individual savings rates typically respond positively to higher interest rates. In addition, higher U.S. interest rates also encourage lenders in other countries to move some of their savings to U.S. markets. Both forces mean that the supply curve for savings is upwardly sloped in most circumstances.