15.1 CHAPTER REVIEW
FACTS AND TOOLS
Question 15.1
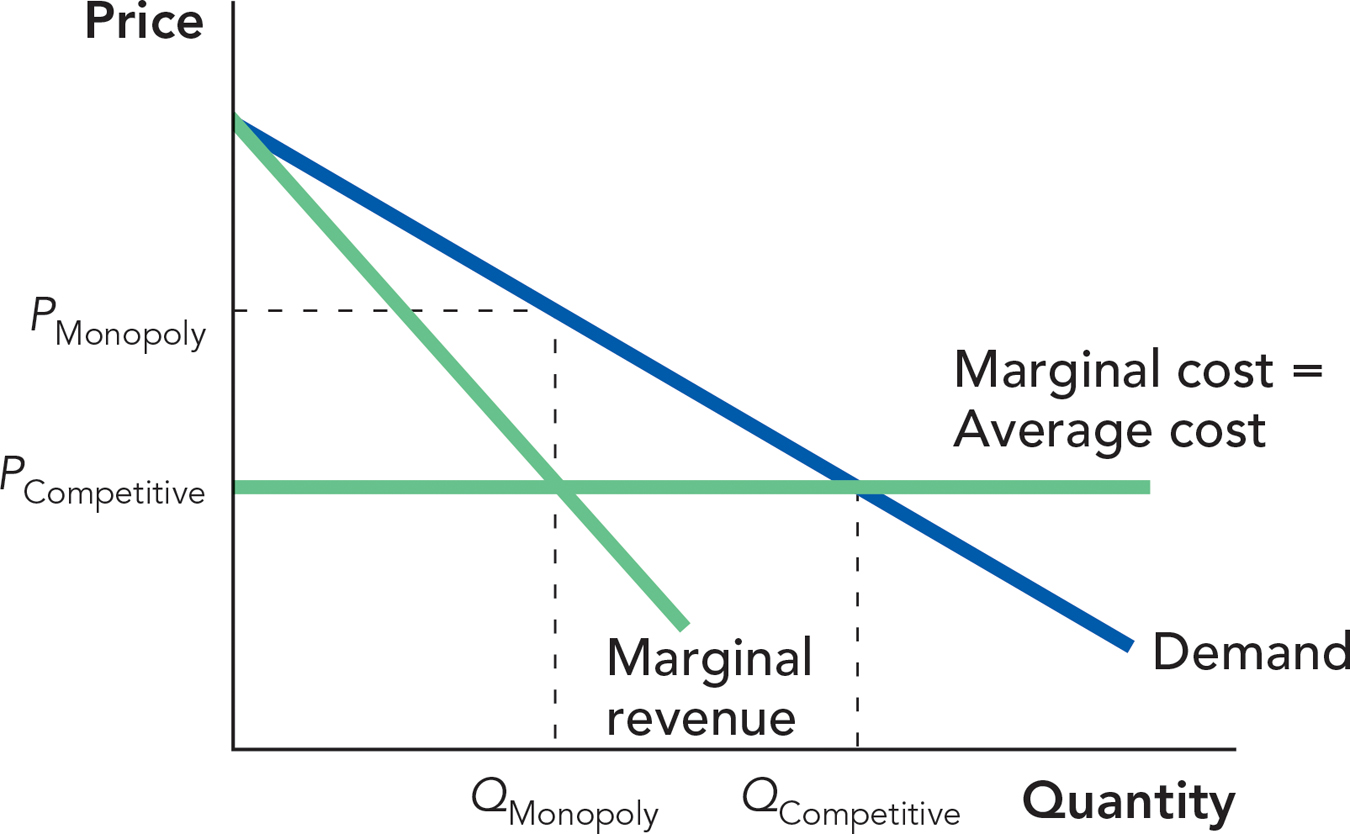
1. Let’s start off by working out a few examples to illustrate the lure of the cartel. To keep it simple on the supply side, we’ll assume that fixed costs are zero so marginal cost equals average cost. We’ll compare the competitive outcome (P = MC) to what you’d get if the firms all agreed to act “as if” they were a monopoly. In all cases, we’ll use terms from the following diagram:
297
First, let’s see where the profits are. Comparing this figure with Figure 15.2, shade the rectangle that corresponds to monopoly profit.
What is the formula for this rectangle in terms of price, cost, and quantity?
Let’s look at the market for one kind of apple: Gala. Assume that there are 300 producers of Gala apples and that MC = AC = $0.40 per pound. In a competitive market, price will be driven down to marginal cost. Let’s assume that when P = MC, each apple grower produces 2 million pounds of apples for a total market production of 600 million pounds. Now imagine that the apple growers form a cartel and each agrees to cut production to 1 million pounds, which drives the price up to $0.70 per pound. Calculate profit per pound and total industry profit if the apple growers behave “as if” they were a monopoly and are able to produce according to the following table:
P Monopoly
Q Monopoly
$0.70/lb
300 million lb
Profit per pound Monopoly
Total industry Profit Monopoly
_________
_________
If a single apple grower broke from the cartel and produced an extra million pounds of apples, how much additional profit (approximately) would this apple grower make?
Question 15.2
2. Take a look at the reasons why cartels collapse presented in this chapter. For each of the following pairs, choose the case where the cartel is more likely to stick together.
An industry where it’s easy for new firms to enter vs. an industry where the same firms stick around for decades.
When the government makes it legal for all the firms to agree on prices vs. when the government makes it illegal for all firms in an industry to agree on prices.
(Note: The Sherman Antitrust Act made the latter generally illegal in 1890, but President Franklin Roosevelt’s National Industrial Recovery Act temporarily legalized price-setting cartels during the Great Depression.)
Cartels where all the industry leaders went to the same schools and live in the same neighborhood vs. cartels where the industry leaders don’t really know or trust each other. (Hint: As Adam Smith said in The Wealth of Nations, “People of the same trade seldom meet together, even for merriment and diversion, but the conversation ends in a conspiracy against the public, or in some contrivance to raise prices.”)
An industry where it’s easy for a firm to sell a little extra product without anyone knowing (e.g., music downloads) vs. an industry where all sales are public and visible (e.g., concert tickets).
Question 15.3
3. The prisoner’s dilemma game is one of the most important models in all of social science: Most games of trust can be thought of as some kind of prisoner’s dilemma. Here’s the classic game: Two men rob a bank and are quickly arrested. The police do not have an airtight case; they have just enough evidence to put each man in prison for one year, a slap on the wrist for a serious crime.
If the police had more evidence, they could put the men away for longer. To get more evidence, they put the men in separate interrogation rooms and offer each man the same deal: If you testify against your accomplice, we will drop all the charges against you (and convict the other guy of the full penalty of 10 years of prison time). Of course, if both prisoners take the deal, the police will have enough evidence to put both prisoners away and they will each get 6 years. And, as noted, if neither testifies, both will get just 1 year of prison time. What’s the best thing for each man to do?
In each cell in the following table, the first number is the number of years Butch will spend in prison, and the second is the number that Sundance will spend in prison given the strategies chosen by Butch and Sundance. If years in prison are minuses, then we can write up the problem like this:
298
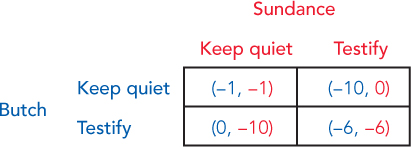
If Sundance keeps quiet, what’s the best choice (highest payoff) for Butch: keep quiet or testify?
If Sundance chooses testify, what’s the best choice for Butch: keep quiet or testify?
What’s the best choice for Butch? What’s the best choice for Sundance?
Using the definition in this chapter, does Butch have a “dominant strategy”? If so, what is it?
What is your prediction about what will happen?
How does this help explain why the police never put two suspects in the same interrogation room? (Note the similarity between this question and the earlier Adam Smith quote.)
Question 15.4
4. Your professor probably grades on a curve, implicitly if not explicitly. This means that you and your classmates could each agree to study half as much, and you would all earn the same grade you would have earned without the agreement. What do you think would happen if you tried to enact this agreement? Why? Which model in this chapter is most similar to this conspiracy?
Question 15.5
5. In many college towns, rumors abound that the gas stations in town collude to keep prices high. If this were true, where would you expect this conspiracy against the public to work best? Why?
In towns with dozens of gas stations or in towns with fewer than 10?
In towns where the city council has many environmental and zoning regulations, making it difficult to open a new gas station, or in towns where there is a lot of open land for development?
In towns where all the gas stations are about equally busy or in towns where half the gas stations are always busy and half tend to be empty?
Question 15.6
6. Suppose you have a suit that needs altering, and you take it to three different tailors in the same mall to get an estimate of the cost of the alterations. All three tailors give you the exact same estimate of $25. What are two different explanations for the similarity of the price quotes? (Hint: One is consistent with competition and one is not.)
THINKING AND PROBLEM SOLVING
Question 15.7
1. Usually, we think of cheating as a bad thing. But in this chapter, cheating turns out to be a very good thing in some important cases.
Who gets the benefit when a cartel collapses through cheating: consumers or producers?
Does this benefit usually show up in a lower price, a higher quantity, or both?
Does cheating increase consumer surplus, producer surplus, or both?
So, is cheating good for the cheaters or good for other people?
Question 15.8
2. Firms in a cartel each have an incentive individually to lower the prices they charge.
Suppose there was a government regulation that set minimum prices. Would this regulation tend to strengthen cartels, weaken them, or have no effect?
Another way that one firm can cheat on a cartel is to offer a higher-quality product to consumers. Suppose there was a government regulation that standardized the quality of a good. Would this regulation tend to strengthen cartels, weaken them, or have no effect?
Question 15.9
3. In the late fifteenth century, Europe consumed about 2 million pounds of pepper per year. At this time, Venice (ruled by a small, tightly knit group of merchants) was the major player in the pepper trade. But after Portuguese explorer Vasco da Gama blazed a path around Africa into the Indian Ocean in 1498, Venice found itself competing with Portugal’s trade route. By the mid-sixteenth century, Europeans consumed 6 to 7 million pounds per year, much of it through Lisbon. After da Gama’s success, the price of pepper fell.
During the fifteenth century, was it likely that a cartel was restricting pepper imports? Why or why not?
If the price of pepper before 1498 had been lower, would da Gama have been more willing or less willing to sail around South Africa’s Cape of Good Hope? Why?
What happened in 1498 that turned a successful cartel into a less successful cartel?
The ruling merchants of Venice had no political power in other parts of Europe. Why is that important in understanding how European pepper consumption more than tripled in just over half a century?
299
Question 15.10
4. In 1890, Senator Sherman (of the Sherman Antitrust Act mentioned earlier) pushed through the legislation that bears his name, which gave the government significant power to “bust up” cartels, presumably in order to increase output. More than a century later, economist Thomas J. DiLorenzo examined the industries commonly accused of being cartels and found those industries increased output by an average of 175% from 1880 to 1890—seven times the growth rate of the economy at the time.
Suppose the industries were conspiring. Indeed, let’s suppose that these cartels grew ever stronger in the decade before the Sherman Act became law. If that were true, would we expect output in these industries to grow by so much? In other words, is DiLorenzo’s evidence consistent with the standard story of the Sherman Antitrust Act?
Question 15.11
5. In 2005, economist Thomas Schelling won the Nobel Prize in economics, in part for his development of the concept of the “focal point” in game theory. Focal points are a way to solve a coordination game. If two people both benefit by choosing the same option but cannot communicate, they will choose the most obvious option, called the focal point. Of course, what’s obvious will vary from culture to culture: whether to wear business attire or just shorts and a T-shirt, whether to use Apple or Microsoft products, whether to arrive at meetings on time or late. In all these cases, having a group agree on one focal point is more important than which particular focal point you all agree on. Therefore, people will look for cultural clues so that they can find the focal point. (Note: Schelling wrote two highly readable books that won him the Nobel Prize: Micromotives and Macrobehavior and The Strategy of Conflict.)
Suppose you are playing a game in which you and another player have to choose one of three boxes. You can’t communicate with the other player until the game is over. One box is blue and the other two are red. If the two of you choose the same box, you win $50, otherwise, you get nothing. Which box do you choose: the blue box or one of the red boxes? Why?
Suppose that you and another player have to write down on a slip of paper any price in dollars and cents between $90.01 and $109.83. If you both write down the same price, you’ll each win that amount of money. If your numbers don’t match, you get nothing. Again, you can’t communicate with the other player until the game is over. What number will both of you probably choose?
Many “slippery slope” arguments are really stories about focal points. In the United States during debates over banning guns or restricting speech, people will argue that any limitation follows a “slippery slope.” What do they mean by that? (Hint: Attorneys often worry about “gray areas” and they prefer “bright line tests.”)
Schelling used the idea of the focal point to explain implicit agreements on the limits to war. Poison gas, for example, was not used in World War II and the agreement was largely implicit. Since focal points have to be obvious, explain why there was no implicit agreement that “some” poison gas would be allowed, but “a lot” of poison gas would not be allowed.
Question 15.12
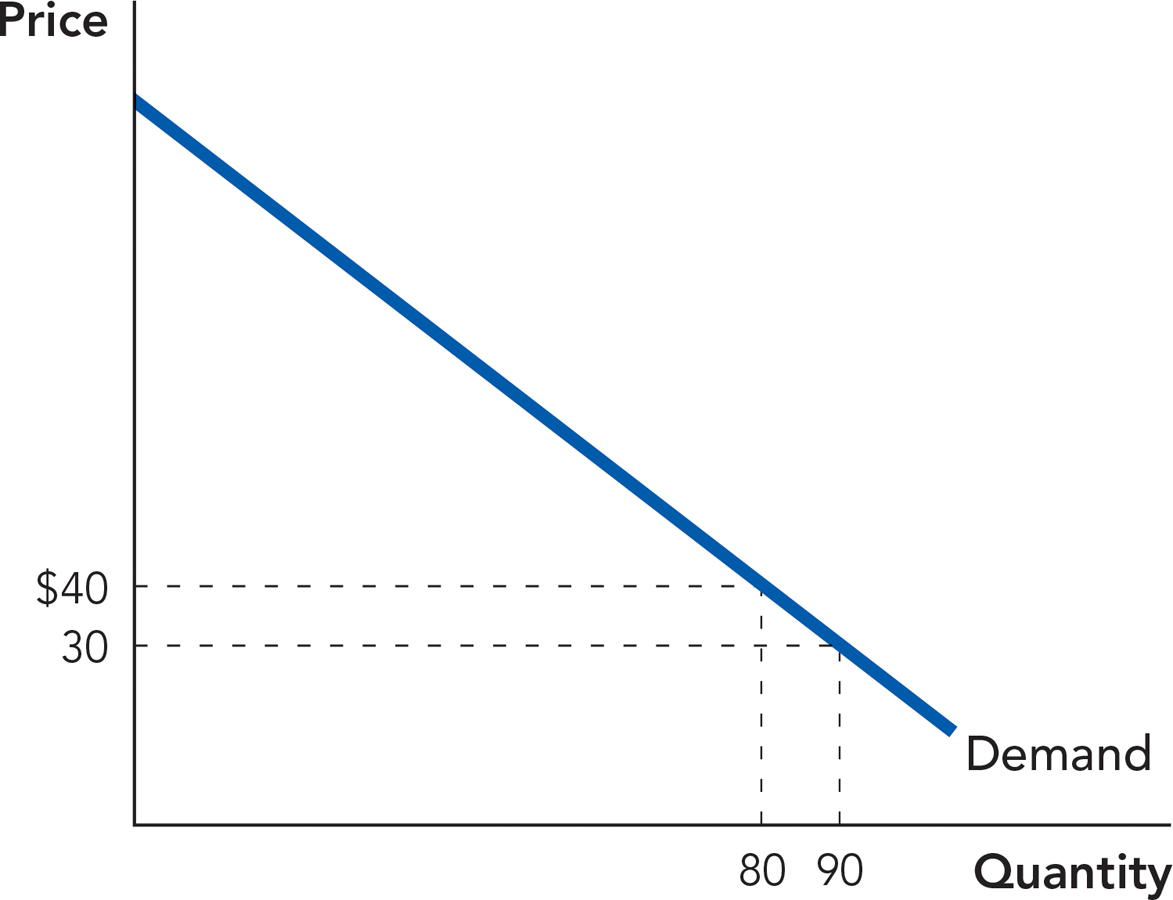
6. Suppose the five landscapers in your neighborhood form a cartel and decide to restrict output to 16 lawns each per week (for a total of 80 lawns in the entire market) in order to keep prices high. The weekly demand curve for lawn-mowing services is shown in the following chart. Assume that the marginal cost of mowing a lawn is a constant $10 per lawn.
300
What is the market price under the cartel’s arrangement? How much profit is each landscaper earning per week under this arrangement?
Suppose one untrustworthy landscaper decides to cheat and increase her own output by an additional 10 lawns. For this landscaper, what is the total increase in revenue from such behavior? What is the marginal revenue per lawn from cheating? Which is higher: the marginal revenue from the extra lawns or the marginal cost?
Is it a good idea for the untrustworthy landscaper to cheat? What considerations, other than weekly profit, might enter into the landscaper’s decision about whether to cheat?
Question 15.13
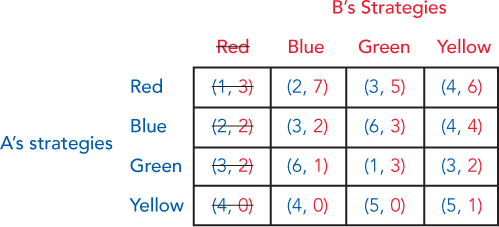
7. Looking for dominant strategies is a great way to find an equilibrium in many games. However, there are also a lot of games where this won’t work because not all players have dominant strategies. If one player has a dominant strategy but the other doesn’t, game theorists remove the first player’s dominated strategies (the strategies that are always worse than some other strategy) and then continue to work toward solving the game with what’s left. Let’s take a look at an example of this. Consider the following payoff table, where the outcomes are written in the form {A’s payoff, B’s payoff}. Each player has four choices, which might make this game seem intimidating, but it’s not.
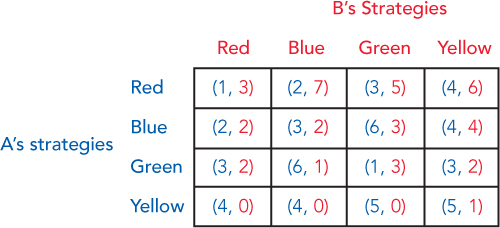
Start off by trying to figure out whether any player has a strategy that is never best, and then eliminate it. The first one is done for you; no matter what move A makes, B’s best response is never to play Red. Since B will never play Red, we don’t even have to consider that as part of the game. Next, figure out if there’s a move A will never make, then B, and so on. What is the equilibrium?
CHALLENGES
Question 15.14
1. The French economist Antoine Cournot developed an interesting model of competition in an oligopoly that now bears his name. In a Cournot oligopoly, all of the firms know that the total output from all firms will determine the price (based on the downward-sloping market demand curve), but they make independent and simultaneous decisions about how much output to produce. Cournot developed this model after observing how a spring water duopoly (two firms) behaved. So let’s look at a duopoly example.
For each firm to decide how much to produce, it must make a guess about how much the other firm is going to produce. Also, the firms basically assume that once the other firm has decided how much to produce, it can’t really change its decision.
Here’s an example. Suppose the market demand curve for gallons of fresh spring water looks like the one in the next table and, to keep things simple, the marginal cost of spring water is zero. If Firm X believes that Firm Y is going to produce 100 gallons of spring water, for example, then Firm X knows that if it produces 0 gallons, the price will be $2.75; if it produces 100 gallons, the price will be $2.50, and so on. Basically, Firm X will face its own demand curve where all of the quantities are lower by 100.
301
|
Market Demand |
|
|---|---|
|
Price |
Quantity Demanded (gal) |
|
$3.00 |
0 |
|
$2.75 |
100 |
|
$2.50 |
200 |
|
$2.25 |
300 |
|
$2.00 |
400 |
|
$1.75 |
500 |
|
$1.50 |
600 |
|
$1.25 |
700 |
|
$1.00 |
800 |
|
$0.75 |
900 |
|
$0.50 |
1,000 |
Based on this demand schedule, calculate the demand schedule that Firm X would face if it suspected Firm Y was going to produce 0, 200, 400, or 600 gallons of spring water. Then, figure out the profit-maximizing amount of spring water for Firm X to produce in response. Fill in the table.
|
If Firm Y produces … |
… then Firm X should produce … |
|---|---|
|
0 gal |
|
|
200 gal |
|
|
400 gal |
|
|
600 gal |
|
What you have just constructed is what economists would call Firm X’s reaction function. Even though Firm X thought about the different choices Firm Y could make, Firm Y is not actually going to choose just any random level of output. In fact, Firm Y has its own reaction function, where it considers how best to respond to what it thinks Firm X is doing. Because both firms have the same zero marginal cost, the two reaction functions are symmetrical. (Thus, Firm Y’s reaction function looks the same, only with “X” and “Y” switched.)
Graph the two reaction functions. Do you notice any points that stand out? Describe why this point represents an equilibrium for both firms.
Question 15.15
2. The following diagram shows the monthly demand for hot dogs in a large city. The marginal cost (and average cost) is a constant $2 per hot dog.
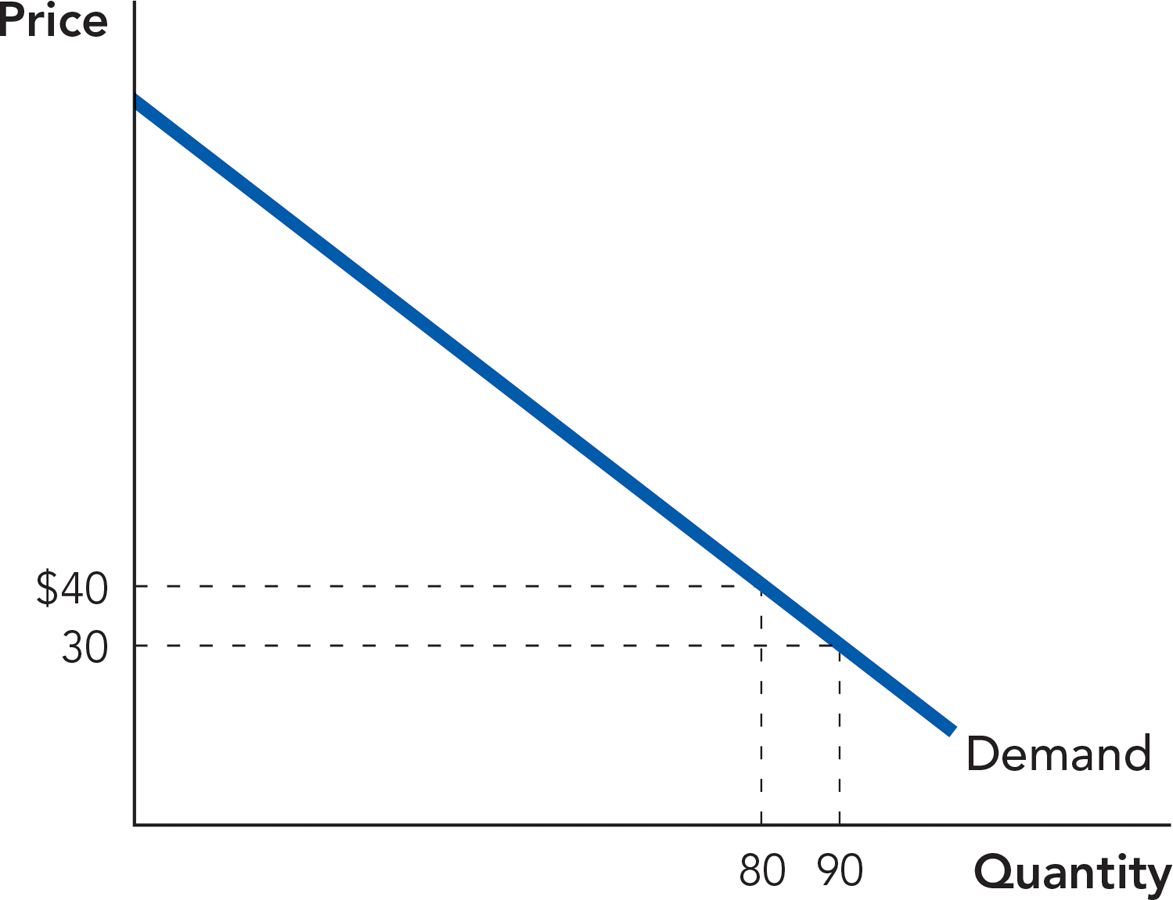
If the market for hot dogs is perfectly competitive, how many hot dogs will be sold per month, and at what price? Suppose there are 100 identical firms in this perfectly competitive market. How many hot dogs is each firm selling, and what are the profits for each firm?
Suppose the market was almost perfectly competitive, so that each firm has some very limited ability to change the price. What would happen if one of the firms in this market reduced its output by one-fifth, and no other firm changed its output? What would happen to the price of a hot dog? How much profit would the firm earn as a result?
Discuss the ability of one firm to reduce output and raise the market price if the market for hot dogs was instead an oligopoly made up of four firms, each initially producing 25,000 hot dogs per month. If only one firm reduced its output by a fifth, what would happen to the price of a hot dog? How much profit could this firm potentially earn?
Compare your answers for parts b and c. What does this tell you about the ability to earn profits in perfect competition vs. oligopoly?
302
!launch! WORK IT OUT
Consider the following demand schedule for Rainbow Looms. Assume that the marginal cost of producing a Rainbow Loom is a constant $2.50.
|
Price ($/Rainbow Loom) |
Quantity Demanded (Rainbow Loom) |
|---|---|
|
$17.50 |
0 |
|
$15.00 |
12 |
|
$12.50 |
24 |
|
$10.00 |
36 |
|
$7.50 |
48 |
|
$5.00 |
60 |
How many Rainbow Looms would be produced under a Rainbow Loom monopoly?
If instead of a monopoly, a two-firm cartel controlled the Rainbow Loom market, how many packs of Rainbow Looms would each firm want to produce in order to maximize industry profits?
Determine whether it would be possible for one of the two firms in the cartel to earn higher profits by producing more than the industry profit-maximizing quantity you calculated in part b.
303