The games examples in this chapter can be solved by looking for a dominant strategy, a strategy that is best regardless of what the other player does. Even in simple games, however, there often isn’t a dominant strategy. Consider a simple game called the Left, Right game. Olaf and Frida must decide whether to drive their cars on the left side of the road or on the right. The payoff for each combination of choices is illustrated in the payoff matrix in Figure A15.1.

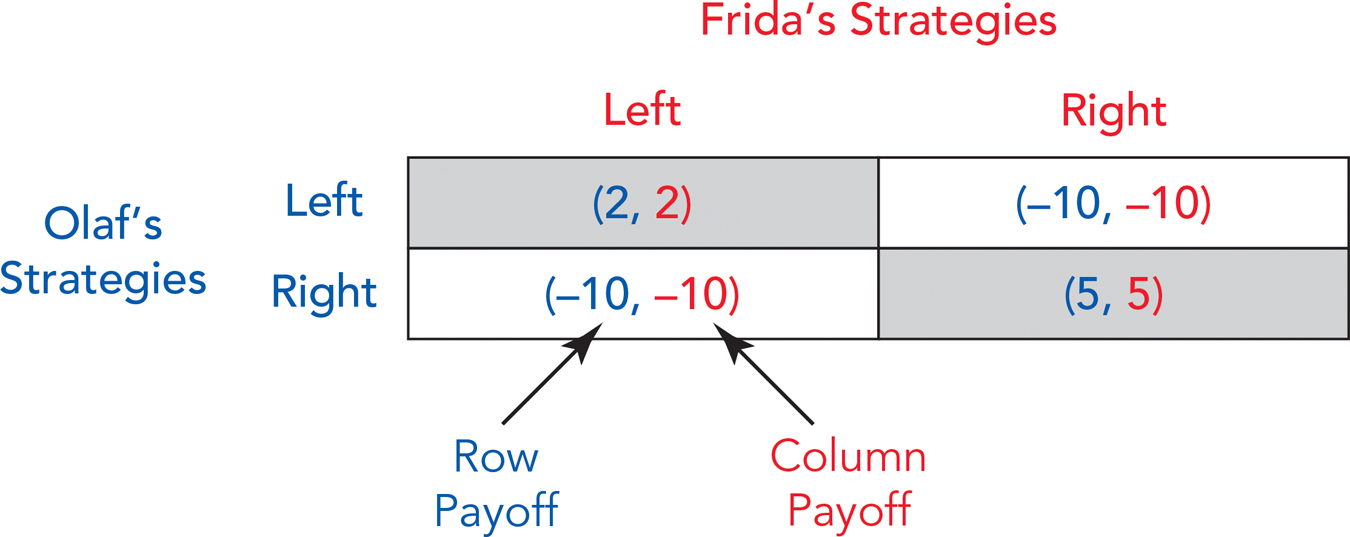
The key point, of course, is that Olaf and Frida have positive payoffs when they both choose Left or when they both choose Right, but it’s a disaster when Olaf chooses Left and Frida chooses Right or vice versa. When Olaf and Frida both choose Left, the payoffs are 2,2, and when Olaf and Frida both choose Right, the payoffs are 5,5. But when Olaf and Frida choose different strategies, either {Left, Right} or {Right, Left}, they end up crashing their cars and the payoffs are −10,−10. So what is the equilibrium to this game?

Unlike in the prisoner’s dilemma, there is no dominant strategy in this game, no strategy that is best for each player regardless of what the other player does. We can still look for equilibria, however, by drawing on the ideas of John Nash. Nash, who was awarded a Nobel Prize for his contributions to game theory and whose life was featured in the movie A Beautiful Mind, defined an equilibrium as a situation in which no player has an incentive to change strategy unilaterally. That is now called a Nash equilibrium.

In the Left, Right game, there are two Nash equilibria. Let’s start by examining the paired strategies {Left, Left}. Is this a Nash equilibrium? If Frida chooses Left, does Olaf have an incentive to change strategy? No. Olaf earns 2 by choosing Left and −10 by switching to Right so if Frida chooses Left, then Olaf does not have an incentive to change strategy. If Olaf chooses Left, does Frida have an incentive to change strategy? No. Frida earns 2 by choosing Left and −10 by choosing Right, so if Olaf chooses Left, Frida does not have an incentive to switch. Since neither player has an incentive to unilaterally change strategy, {Left, Left} is a Nash equilibrium. By similar reasoning, you should be able to show that {Right, Right} is also a Nash equilibrium.

304

Is {Right, Left} a Nash equilibrium? If Frida chooses Left, does Olaf have an incentive to change strategy? Yes. Olaf earns −10 by choosing Right and 2 by switching to Left, so if Frida chooses Left then Olaf would have an incentive to change strategy to Left. Since at least one of the parties has an incentive to change strategy, {Right, Left} cannot be a Nash equilibrium (in fact, Olaf and Frida both have an incentive to change but we need show only that one of them has an incentive to change to show that a situation is not a Nash equilibrium). By similar reasoning you should be able to show that {Left, Right} is also not a Nash equilibrium.

If a player can increase his or her payoff by changing strategy, they probably will change it. So game theory predicts that the outcome of a game will be a Nash equilibrium. If there is more than one equilibrium, however, game theory alone doesn’t tell us which equilibrium will be the outcome. In the Left, Right game, {Left, Left} is a Nash equilibrium and so is {Right, Right}, and indeed when we look around the world we see people in some countries driving on the right and in other countries such as Great Britain and Australia driving on the left. Why the difference? Probably nothing more than accidents of history or other random factors.

According to the payoff matrix, Olaf and Frida earn 2,2 in the {Left, Left} equilibrium and 5,5 in the {Right, Right} equilibrium. In our world, it is in fact better to drive on the right since more countries drive on the right and more cars are built for driving on the right. If Olaf and Frida were the only two players and if they played this game repeatedly (say they had to choose Right or Left every day), then it would be a good bet that they would eventually end up at the {Right, Right} equilibrium since it has a higher payoff for both. But if there are many Olafs and Fridas and less opportunity for experimentation, the players might become stuck in the {Left, Left} equilibrium, as have Great Britain and Australia. Even with many Olafs and Fridas, a switch might very occasionally be possible. In fact, on September 3, 1967, Sweden switched from driving on the left to driving on the right! Good for Olaf and Frida.

In addition to defining the concept of a Nash equilibrium, John Nash proved that all games have at least one Nash equilibrium (sometimes in what are called mixed strategies, strategies requiring randomization). Thus, the Nash equilibrium concept greatly expanded the number of games that economists could analyze and it has become a standard tool in economics.

305