How to Compare Apples and Oranges
Despite being warned not to, consumers do compare apples and oranges. In fact, consumers have to compare apples, oranges, and every other good if they are to spend their limited budget wisely.
Marginal utility is the change in utility from consuming an additional unit.
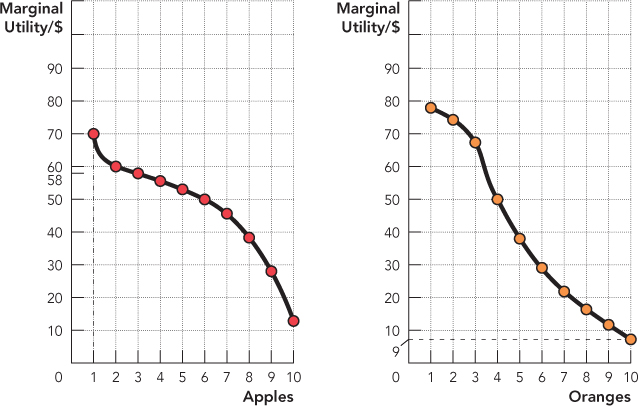
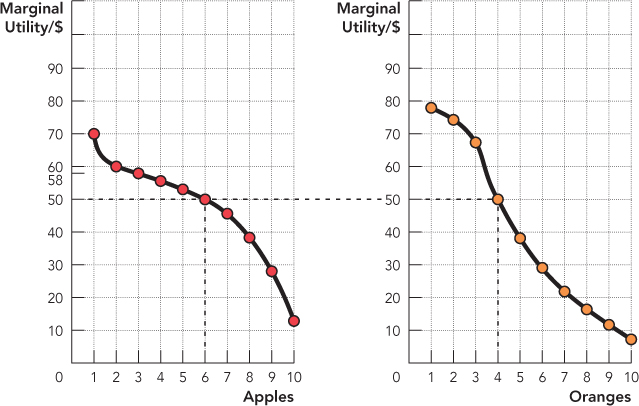
Apples and oranges both produce value or, in economic terms, “utility” for the consumer. We call the increase in utility generated by an additional apple the marginal utility of an apple and denote it MUA. We will assume that marginal utility is diminishing. Diminishing marginal utility means that the first apple is great, the second good, the third not bad, and so on. Figure 25.1, for example, shows a marginal utility curve for apples on the left and a marginal utility curve for oranges on the right. In the figure, the marginal utility of the first apple is 70 “utils,” the second is 60 utils, the third is 58 utils, and so forth.
Diminishing marginal utility means that each additional unit of a good adds less to utility than the previous unit.

466
But apples and oranges aren’t free. There is a price for apples, which we write as PA, and there is a price for oranges, which we write as PO. A consumer might love oranges more than any other fruit, but if the price of oranges is high, that consumer may buy apples. The real problem a consumer faces, therefore, is not to choose apples and oranges directly, but to choose how many dollars to spend on apples and how many dollars to spend on oranges. Apples and oranges are two alternative ways of generating utility from dollars. So how should a consumer allocate her dollars between apples and oranges?
As usual, the way to solve this problem is to think on the margin. Each additional dollar allocated to apples generates a certain amount of utility. For example, if the marginal utility of an apple is 70 and the price of apples is $2 per apple, then the marginal utility per dollar spent on apples is 35. More generally, the marginal utility per dollar spent on apples is 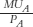 To simplify, if we suppose that PA = PO = $1, then we can use the same figure as before, except now the axis is in terms of marginal utilities per dollar.
To simplify, if we suppose that PA = PO = $1, then we can use the same figure as before, except now the axis is in terms of marginal utilities per dollar.
So which combination of apples and oranges maximizes utility? It’s easiest to begin with a bundle that doesn’t maximize utility. Once we understand why such a bundle doesn’t maximize utility, the solution to the problem will become clear.
Consider Figure 25.2 and suppose that the consumer has $10 in income and she buys 10 oranges and no apples. From the right panel, we can see that the 10th orange is generating 9 utils per dollar. Now consider how much utility would be generated by consuming one dollar less of oranges and one dollar more of apples. From the left panel, we can see that the first dollar spent on apples will generate 70 utils. Thus, by consuming one fewer orange (–9 utils) and one more apple (+70 utils), the consumer can get an increase of 61 utils in total utility.
467
Keep following this logic. Should the consumer consume 9 oranges and 1 apple? No. Notice that the marginal utility per dollar of the second apple exceeds the marginal utility per dollar of the ninth orange, so the consumer can increase total utility by shifting another dollar of consumption away from oranges and toward apples.
In other words, if the marginal utility per dollar of apples is higher than the marginal utility per dollar of oranges, then the consumer gets more “bang from a buck” spent on apples than on oranges. Thus, she should buy more apples and fewer oranges:
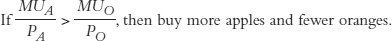
By exactly the same logic, if the marginal utility of apples were less than that of oranges, then the consumer gets more bang from a buck spent on oranges. Thus, she should buy fewer apples and more oranges, that is,
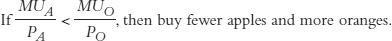
Putting these two conditions together, we find that there is only one condition when the consumer cannot increase utility by adjusting her spending, that is, only one condition when the consumer is maximizing utility:

468
Figure 25.3 shows that if one follows this logic, the point of maximum utility for the consumer is to consume 6 apples and 4 oranges.
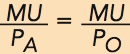 .
.We have derived our rule for just two goods, but the idea is perfectly general. Thus, to maximize utility, the optimal consumption rule says a consumer should allocate his or her spending so the marginal utility per dollar is equal for all purchases:
The optimal consumption rule says that to maximize utility, a consumer should allocate spending so that the marginal utility per dollar is equal for all purchases.
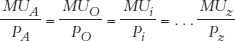
Even if you don’t consciously think of the “marginal utility per dollar of an apple” as a specific number, the rule tells us that to maximize utility, we should spend our bucks until the bang from a buck is the same for all purchases.