If the owner wants to maximize profit, how many barrels of oil should a stripper oil well produce? Profit is total revenue minus total cost, so the owner wants to maximize the difference between total revenue and total costs.

Profit = ∏ = Total revenue – Total cost

Total revenue is fairly easy to understand. Total revenue is simply price times quantity (P × Q). If the price of oil is $50 per barrel, then total revenues are $50 per day if 1 barrel is produced per day, $100 if 2 barrels are produced, $150 if 3 barrels are produced, and so forth.

Total costs, however, are more tricky. First, we have to remember that total costs include opportunity costs, not just money costs. Second, understanding the profit maximization decision will require us to distinguish among many different costs—not just total costs, but also average costs, marginal costs, fixed costs, and a few others. Keeping all these different costs straight will take some effort.

198

Total costs include explicit money costs and also implicit opportunity costs, the costs of foregone alternatives. Imagine that Lian runs a flower shop. Each month she spends $10,000 buying flowers from a wholesaler. The cost of flowers is an explicit cost of running her shop, like rent and electricity, which she pays out of pocket by writing a check. But these are not her only costs. If Lian weren’t selling flowers, let’s suppose that she could be working as a patent attorney earning $7,000 a month. Lian is giving up something of value when she works as a florist, namely the opportunity to earn $7,000 a month—that’s also a cost of running a flower shop, even though she is not writing anybody a check. It is an implicit cost. When deciding whether she would rather be a florist or a patent attorney, for example, Lian needs to take into account all of her costs, including opportunity costs.

Here is another example. Imagine that Alex and Tyler each decide to drill an oil well in their backyard, which costs $200,000. Alex borrows the $200,000 from a bank at a 5% annual rate of interest so Alex must pay the bank $10,000 per year ($10,000 = 0.05 × $200,000). Tyler pays the $200,000 out of a small inheritance he received from a rich uncle. Each well produces $15,000 worth of oil annually. Which well is more profitable?

At the end of every year, Alex pockets $5,000 ($15,000 in revenue minus $10,000 in interest cost), while Tyler pockets $15,000. It’s tempting to conclude that Tyler’s well is more profitable, but that would be a mistake. Tyler could have left his $200,000 in the bank, and at a 5% rate of interest, he would have earned $10,000 a year in income. Tyler’s opportunity cost is the $10,000 in income he gave up when he invested his money in drilling the oil well. Thus, once we take into account all costs, including opportunity costs, Alex and Tyler’s wells are equally profitable.

The economic definition of profit differs from the accounting definition of profit because accountants typically don’t take into account all opportunity costs. As a result, economic profits are typically less than accounting profits. Why is the distinction between accounting and economic profit important? Because firms want to maximize economic profit, not accounting profit.

Let’s look again at Alex and Tyler and their oil wells. Suppose that the price of oil fell, so that instead of earning revenues of $15,000, each oil well earned revenues of just $6,000. In Alex’s case, he has to pay the bank $10,000 in interest annually so it’s obvious that Alex is losing $4,000 a year. In reality, we know that from an economic point of view, Tyler is in exactly the same situation—his oil well is also economically unprofitable. If Tyler just looks at his accounting profits, however, he will see a profit of $6,000, which may cause him to be complacent and perhaps even to invest more in the oil industry!

Calculating economic profit is important for entrepreneurs who must always think about the future. Is this the best use of our firm’s assets? What am I giving up by following this strategy? Could these assets be used to make more profit if I used them in another way? Economic profit is also what stock market investors want to keep an eye on. Careful stock market investors, for example, will look beyond accounting profits to economic profit to see whether a firm is truly using its assets in the most profitable way possible. Firms that are not using their assets in the most profitable way possible are good targets for takeovers.

199

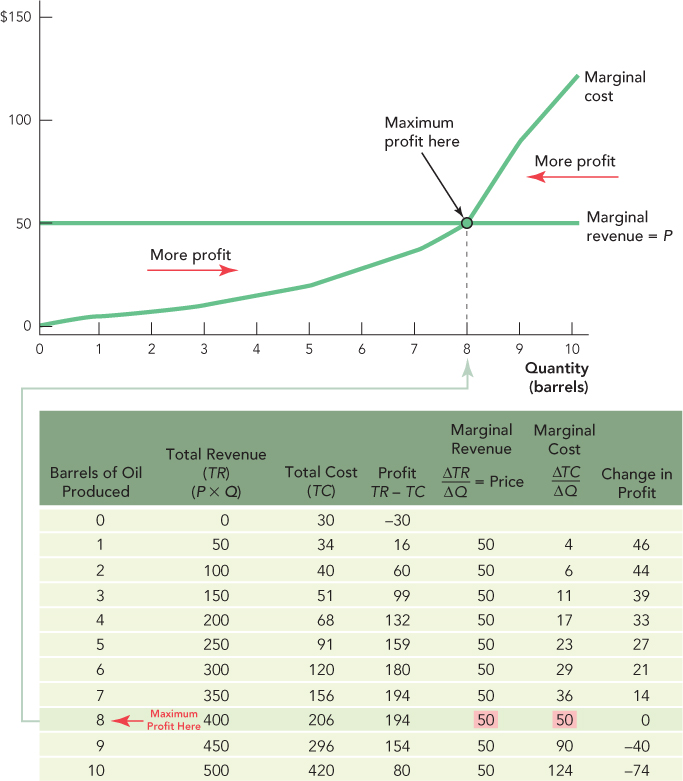
Okay, from here on, we will take it for granted that our measure of total costs includes opportunity costs. Let’s now return to a typical stripper oil well. The table in Figure 11.2 shows total revenues and total costs as barrels of oil produced increase from 0 to 10 barrels.

Total cost is simply the cost of producing a given quantity of output. Let’s break total cost into two components. To produce oil, the firm must drill the well and then it must pump the oil out of the ground and deliver it to customers. Let’s assume that the firm rents the land on which it drills the well for $30 per day (we use rent per day to make a comparison with barrels of oil produced per day more convenient). Notice that the firm must pay $30 per day even if it pumps no oil; hence, the entry in the table for Total Cost for 0 barrels is $30. In fact, the firm must pay $30 per day in rent no matter how many barrels of oil it produces. Thus, we say that the firm has $30 per day of fixed costs, costs that do not vary with output.

The firm must pay additional costs when it runs the oil pump. To pump the oil, the firm must pay for electricity, maintenance, costs for the barrels to store the oil, trucking costs to deliver the oil, and so forth. These costs are called variable costs, since they vary with output. Total costs are therefore equal to fixed costs plus variable costs.

Total cost (TC) = Fixed costs (FC) + Variable costs (VC)

Profit is the difference between total revenue and total cost, and it is shown in the fourth column. Thus, to find the maximum profit, one method is to look for the quantity that maximizes TR – TC. Using the table in Figure 11.2, we can see that the profit maximizing quantity is 8 barrels of oil per day.

It turns out to be useful, especially in order to create graphs, to use a second method to find the quantity that maximizes profit. Instead of looking at total revenue and total cost, we compare the increase in revenue from selling an additional barrel of oil, called marginal revenue, to the increase in cost from selling an additional barrel, called marginal cost. To maximize profit, we will show that the owner wants to keep producing oil so long as Marginal revenue > Marginal cost, which means that the last drop of oil the firm produces should be the one where Marginal revenue = Marginal cost. Let’s walk through this argument.

Marginal revenue is the change in total revenue from selling an additional barrel of oil. Suppose that the price of a barrel of oil is $50. Then what is marginal revenue? If the owner sells an additional barrel of oil, his or her revenues increase by $50, so marginal revenue is just equal to $50, the price. That was easy because we assumed that the price of oil doesn’t change as the firm sells more barrels; in other words, we used our assumption that a stripper oil well is in a competitive industry and thus faces a perfectly elastic demand curve at the market price. Thus, we have a simple rule: For a firm in a competitive industry, MR = P.

Marginal cost is the change in total cost from producing an additional barrel of oil. The owner of a small oil well has some choice about whether to produce a little bit more or a little bit less. The owner, for example, can increase the pump rate and produce more oil per day but only by spending more on electricity, maintenance, and the more frequent pickup and shipping of the oil. The extra costs that come with a little additional production are called marginal costs. Notice, for example, that if the well produces 2 barrels of oil per day, then Total cost = $40, and if the well produces 3 barrels per day, then Total cost = $51. Thus, producing the third barrel of oil increases costs by $11, that is, the marginal cost of the third barrel of oil is $11.

200

At some point, marginal costs must increase because you can only get so much blood out of a stone and only so much oil out of rock. The well, for example, cannot be pumped more than 24 hours a day. As the well reaches capacity, the marginal cost of an additional barrel approaches infinity!

We can now use the data in Figure 11.2 to find the profit-maximizing quantity using our second method. The owner should keep producing additional barrels so long as the revenue from producing an additional barrel exceeds the cost of producing an additional barrel. The first barrel of oil that the firm produces adds $50 to revenue and $4 to costs, so MR > MC, and by producing that barrel, the firm can add $46 to profit. On the second barrel, the marginal revenue is $50 and the marginal cost is $6, so producing that barrel adds $44 to profit. Following through on this logic, we can see that each additional barrel of oil adds to profit up until the eighth barrel. If the firm produces the ninth barrel of oil, however, it adds $50 to revenue but $90 to costs, so the firm will not want to produce the ninth barrel. Thus, the profit-maximizing quantity is 8 barrels of oil. Notice that the profit-maximizing quantity is where MR = MC and since MR = P for a competitive firm, we can also say that the profit-maximizing quantity for a competitive firm is where P = MC.

201

Students are often confused by why economists say that the profit-maximizing output is 8 barrels instead of 7 barrels. Why produce the eighth barrel where P = MC and therefore there is no addition to profit? Consider the graph above the table. Notice that wherever P > MC, producing additional barrels means more profit, and wherever MC > P, producing fewer barrels means more profit. Now think about producing oil not in barrels but in drops. Then the graph says that at 7.9999 barrels, you still want to add a drop or two, but at 8.0001 barrels, you want to take away a drop or two. The reason we say profit is maximized where P = MC is that P = MC is the “just right” point between too little and too much.

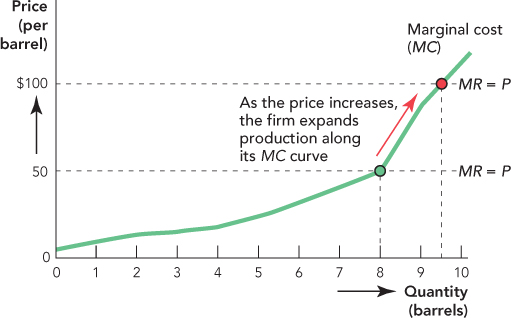
As the price changes, so does the profit-maximizing quantity. When the price is $50, the profit-maximizing quantity is 8. If the price of oil rises to $100 per barrel, then the firm will expand production. But by how much? The firm will expand until it is once again maximizing profit when P = MC. In Figure 11.3, we show how the firm expands production along its MC curve as the price of oil increases from $50 to $100 per barrel.

We have now answered our second question: To maximize profit, the firm should produce the quantity such that MR = MC, which for a firm in a competitive industry means produce up until P = MC.

202