We know from the previous chapter that a firm in a competitive industry increases output until P = MC. What’s even more important is that every firm in the same industry faces the same price. Thus, in a competitive market with N firms, the following will be true:

P = MC₁ = MC₂ = … = MC_N

where MC₁ is the marginal cost of firm 1, MC₂ is the marginal cost of firm 2, and so forth. To understand the importance of this condition, let’s briefly consider a seemingly different problem. Suppose that you own two farms on which to grow corn. Farm 1 is in a hilly region that is costly to seed and plow. Farm 2 is on land ideal for growing corn. The marginal cost of growing corn on each of these farms is illustrated in Figure 12.1.

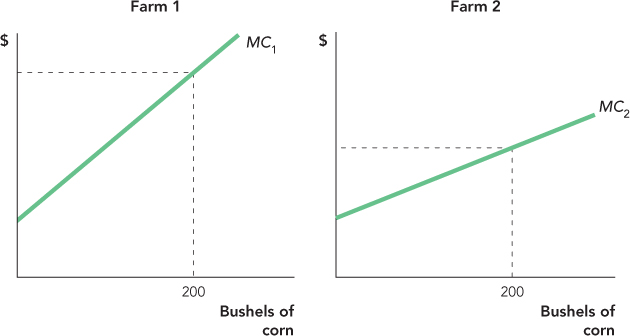
Let’s say that you would like to grow 200 bushels. It might seem that the lowest-cost way to produce 200 bushels is to produce all 200 bushels on Farm 2. After all, the marginal costs of production on Farm 2 are lower than on Farm 1 for any level of output.

Assume that you did produce all 200 bushels on Farm 2 and no bushels on Farm 1. Can you see a way of lowering your total costs of production?

Let’s think in marginal terms. Instead of producing all 200 bushels on Farm 2, what would happen to your total costs of production if you produced, say, 197 bushels on Farm 2 and 3 bushels on Farm 1? Notice from Figure 12.2 that when you produce less on Farm 2, your costs of production decrease by the shaded area labeled A—this is the marginal cost of producing those last few bushels on Farm 2. By instead producing those bushels on Farm 1, your costs increase by area B, the marginal cost of production on Farm 1. But area B is less than area A, so by switching some production from Farm 2 to Farm 1, your total costs of producing 200 bushels of corn goes down.

227

How far can you extend this logic? Clearly, you should continue producing fewer bushels on Farm 2 and more on Farm 1 if the marginal costs of production on Farm 2 exceed those on Farm 1; that is, produce less on Farm 2 and more on Farm 1 if MC₂ > MC₁. By the same logic, you should switch production from Farm 1 to Farm 2 if MC₁ > MC₂. Put these two statements together and it follows that the way to minimize the total costs of production is to produce just so much on each farm so that the marginal costs of production are equalized, MC₁ = MC₂. In the bottom panel of Figure 12.2, we show that the cost-minimizing way to produce 200 bushels of corn is to produce 75 bushels on Farm 1 and 125 bushels on Farm 2.

Now comes the really important part. If you own both farms, you can act as a “central planner” and allocate production across the two farms so that the marginal costs of production are equal and thus the total costs of production are minimized. But now suppose that Farm 1 is in North Carolina and Farm 2 is in Iowa, and let’s say Farm 1 is owned by Sandy and Farm 2 by Pat. Let’s further suppose that Sandy and Pat will live their entire lives without ever meeting. Is there any way to organize production so that the output is split in exactly the way that you would split it if you owned both farms? Yes, there is.

228

Sandy and Pat sell their corn in the same market so each of them sees the same price of corn. How will Sandy maximize profits? How will Pat maximize profits? To maximize profits, Sandy will set P = MC₁ and Pat will set P = MC₂, but this means that MC₁ = MC₂! But we know that if P = MC₁ = MC₂, then the total costs of production are minimized. Amazingly, in pursuit of their own profit, Sandy and Pat will allocate output across their two farms in exactly the way that a central planner would to minimize the total costs of production!

It’s remarkable that a free market could mimic an ideal central planner. What’s even more remarkable is that a free market can allocate production across the two farms to minimize total costs even when an ideal central planner could not! Imagine, for example, that only Sandy knows MC₁ and that only Pat knows MC₂. For a free market, this is no problem, and Sandy and Pat, each acting in their own self-interest, choose the output levels that minimize total costs. But a central planner cannot allocate production correctly if it lacks knowledge of MC₁ and MC₂.

The insight that a free market minimizes the total costs of production is one of the most surprising and deepest in all of economics. In a famous phrase in The Wealth of Nations, Adam Smith described a similar situation saying that each individual “in this, as in many other cases, [is] led by an invisible hand to promote an end which was no part of his intention.” Sandy and Pat don’t intend to minimize the total costs of producing 200 bushels of corn; they intend only to make a profit. But this beneficial outcome is the result of their action. Indeed, until Adam Smith and other economists began to study markets, not only did no one intend to minimize industry costs, no one even knew that individuals acting to maximize their own profits would minimize industry costs.

Friedrich Hayek, a Nobel Prize–winning economist we discussed in Chapter 7, said that properties like the minimization of the total costs of production were “products of human action but not of human design.”

Invisible Hand Property 1 says that even though no actor in a market economy intends to do so, in a free market P = MC₁ = MC₂ = … = MC_N and, as a result, the total industry costs of production are minimized.

Invisible Hand Property 1 provides another perspective on free trade. In Chapter 9, we explained how free trade increased wealth by letting the United States buy goods from the lowest-cost producers. We can now see this in another way. Remember that costs are minimized when MC₁ = MC₂ so costs are not minimized when MC₁ ≠ MC₂. Now imagine that Farm 1 and Farm 2 are in different countries with no free trade between them. Sandy and Pat, therefore, face different prices for corn. Since Sandy and Pat face different prices, MC₁ ≠ MC₂ and thus the total costs of producing corn cannot be at a minimum.