CHAPTER REVIEW
FACTS AND TOOLS
Question 12.4
1. Entrepreneurs shift capital and labor across industries in pursuit of profit. Let’s look at this a little more closely. Suppose there are two industries: a high-profit industry, Industry H, and a low-profit industry, Industry L. Answer the following questions about these two industries.
If the two industries have similar costs, then what must be true about prices in the two industries?
What does your answer to part a imply about the value of the output in the two industries?
If labor and capital are moved from Industry L to Industry H, what is given up? What is gained?
Suppose instead that the prices in the two industries were identical. In this case, what must be true about the costs in the two industries?
What does your answer to part d imply about the amounts of capital and labor required to produce one unit of output in each industry?
If labor and capital are moved from Industry L to Industry H, are more units of output lost in Industry L or gained in Industry H?
Question 12.5
2. Suppose that two industries, the pizza industry and the calzone industry, are equally risky, but rates of return on capital investments are only 5% in the pizza industry and 8% in the calzone industry.
Which way will capital flow—from the pizza industry to the calzone industry, or from the calzone industry to the pizza industry?
Question 12.6
3. We’ve claimed that the efficient way to spread out work across firms in the same industry is to set the marginal cost of production to be the same across firms. Let’s see if this works in an example.
Consider a competitive market for rolled steel (measured by the ton) with just two firms: SmallCo and BigCo. If we wanted to be more realistic, we could say there were 100 firms like SmallCo and 100 firms like BigCo, but that would just make the math harder without generating any insight. The two firms have marginal cost schedules like this:
|
Q |
Marginal Cost |
|
|---|---|---|
|
SmallCo |
BigCo |
|
|
1 |
$10 |
$10 |
|
2 |
$20 |
$10 |
|
3 |
$30 |
$10 |
|
4 |
$40 |
$10 |
|
5 |
$50 |
$20 |
|
6 |
$60 |
$30 |
|
7 |
$70 |
$40 |
|
8 |
$80 |
$50 |
We’ll ignore the fixed costs of starting up the firms just to make things a little simpler. What is the total cost at each firm of producing each level of output? Fill in the table.
Q
Total Cost
SmallCo
BigCo
1
$10
$10
2
$30
$20
3
$60
4
5
6
7
8
What’s the cheapest way to make 11 tons of steel? 5 tons?
What would the price have to be in this competitive market for these two firms to produce a total of 11 tons of steel? 5 tons?
Suppose that a government agency looked at BigCo and SmallCo’s cost curves. Which firm looks like the low-cost producer to a government agency? Would it be a good idea, an efficient policy, for the government to shut down the high-cost producer? In other words, could a government intervention do better than the invisible hand in this case?
Let’s make part d more concrete: What would the total cost be if BigCo were the only firm in the market, and it had to produce 7 tons of rolled steel? What would marginal and total costs be if SmallCo and BigCo let the invisible hand divvy up the work between them?
Question 12.7
4. Let’s review the basic mechanism of the elimination principle.
When demand rises in Industry X, what happens to profits? Do they rise, fall, or remain unchanged?
When that happens, do firms, workers, and capital tend to enter Industry X, or do they tend to leave?
Does this tend to increase short-run supply in Industry X or reduce it?
In the long run, after this rise in demand, what will profits typically be in Industry X?
THINKING AND PROBLEM SOLVING
Question 12.8
1. The elimination principle discussed in this chapter tells us what we can expect in the long run from perfectly competitive markets: zero (normal) profits across industries. If this were the case, and this fate were unavoidable, going into business would seem to be a fairly dismal choice, given that the end result of normal profits is known right out of the gate. Despite this, we constantly see entrepreneurs working hard to earn profits. Is this a waste of time, given what we know about the elimination principle? Is the fate of zero profit unavoidable? What would Joseph Schumpeter say about all of this?
Question 12.9
2. How can the market mechanism guarantee that the marginal cost of production will be the same across all firms if those firms have different owners, are in different locations, and have unique cost functions known only to the firms themselves? Why don’t these different firms need to have one shared owner or one shared manager to coordinate this “equal marginal cost” condition?
Question 12.10
3. We’ve seen already from this chapter that dividing up output over multiple producers—even when one has higher costs than the other—can lead to lower industry costs, so long as output is divided up such that MC1 = MC2 = MCN. You’ve already done some practice in Facts and Tools question 3 with cost functions presented as tables. Let’s try to see how this works graphically.
Take a look at the following two marginal cost functions:
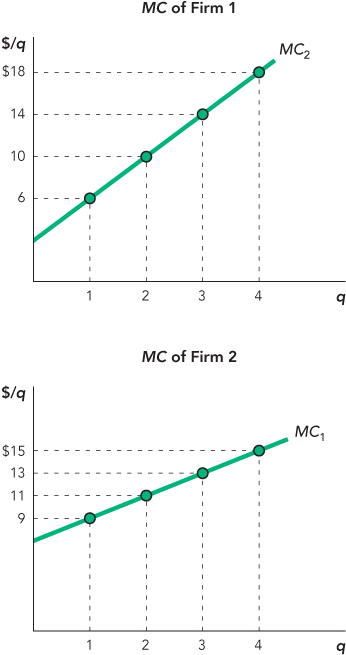
Based on the graphs of these two marginal cost functions, fill in the table below, for industry-wide marginal cost, assuming that production is divided up among the two firms according to Invisible Hand Principle 1. Then, create a graph of the industry marginal cost curve. To help you get started, take a look at the table and answer the following questions. Which firm produces the first unit of industry output? Which firm produces the second unit of industry output? Why?
|
Quantity |
Industry-Wide MC |
|---|---|
|
1 |
$6 |
|
2 |
$9 |
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
Question 12.11
4. In the process of creative destruction, what gets destroyed?
Firms
Workers
Machines
Buildings
Business Plans
Valuable relationships
Or some combination of these? The chapter itself contains quite a few ideas about how to answer this question, but you’ll have to think hard about the “opportunity cost” for each item on the list.
Question 12.12
5. Every year, American television introduces many new shows, only about one-third of which survive past their first season.2 The few shows that last, however, prove to be very profitable.
How does creative destruction explain why studios bother to make new shows if most of them will fail?
In the Summer of 2002, American Idol premiered on television and became immensely popular. How did FOX and other networks respond to this surprise hit?
What happened over the next several years to profits from American Idol? You don’t need to check FOX’s financial statements to get the answer; use the elimination principle!
Question 12.13
6. Let’s suppose that the demand for allergists increases in California. How does the invisible hand respond to this demand? There is more than one correct answer to this question: Try to come up with two or three.
CHALLENGES
Question 12.14
1. Let’s take a look at Invisible Hand Principle 2 in action using a mathematical example. Suppose an industry is characterized by the equations in the following table. (We’re going to assume all individual firms are identical to make this problem a little simpler.)
|
Demand |
QD = 100 − 2P |
|
Individual firm’s supply |
qS = 0.5 + 0.1P |
|
Market supply with n firms |
QS = n × qS = 0.5n + 0.1nP |
|
Individual firm’s average cost |
AC = 5qS − 5 + (24.2/qS) |
Suppose 24 firms are in this industry. What is the equation for market supply? What are the equilibrium price and quantity (this can be found by setting QD = QS)? How much profit is each firm earning? According to the elimination principle, what should occur in this industry over time?
Suppose 35 firms are in this industry. Answer the same questions from part a.
The elimination principle says that profits will be eliminated in the long run, which means that AC = P. Using that fact, figure out how many firms will be in this industry in the long run (solve for n).
WORK IT OUT
Now let’s take a look at the equations for the marginal cost functions that are graphed in Thinking and Problem Solving question 3, and see if we can combine them into one equation for industry-wide marginal cost. This is what the two equations for the graphs in the question look like:
MC1 = 2 + 4q1
MC2 = 7 + 2q2
Can you create an industry marginal cost equation that shows MCTotal as a function of qTotal instead of just q1 or q2?
First, solve both equations for q.
Now, replace MC1 and MC2 with MCTotal, since Invisible Hand Principle 1 tells us that marginal cost will be equal for all of the firms in the industry.
Next, write an equation for qTotal, which is just q1 + q2.
Finally, solve the equation for MCTotal. Now you have created an industry marginal cost function from the cost functions of two different firms in the industry. (If you compare this equation to your answers for Thinking and Problem Solving question 3, you’ll see that the marginal cost is a little different when you use the equation. This is, in part, because this equation assumes you can produce partial units at either firm, whereas your graph was based on the assumption that only whole units were produced.)