CHAPTER REVIEW
FACTS AND TOOLS
Question 25.5
1. The table at right shows the marginal utility a consumer receives from the weekly consumption of On-Demand movie rentals and Thai takeout meals. One On-Demand movie rental costs $5, and Thai takeout costs $10 per meal. Suppose this consumer is currently (for some reason) eating Thai takeout 10 times per week and is spending all of her $100 income, so that she has no money left over for movie rentals. Is the consumer maximizing utility?
|
On-Demand Movies |
Marginal Utility |
Thai Takeout Meals |
Marginal Utility |
|---|---|---|---|
|
1 |
50 |
1 |
50 |
|
2 |
30 |
2 |
45 |
|
3 |
20 |
3 |
40 |
|
4 |
15 |
4 |
35 |
|
5 |
10 |
5 |
30 |
|
6 |
8 |
6 |
25 |
|
7 |
6 |
7 |
20 |
|
8 |
4 |
8 |
15 |
|
9 |
2 |
9 |
10 |
|
10 |
1 |
10 |
5 |
Question 25.6
2. Imagine that for the past two years, you’ve consumed only two goods: lattes and scones. As you’re probably aware, prices tend to go up over time. If the price of your latte increased from $2 to $3 over the last two years, and the price of scones increased from $1.50 to $2.25, what impact would this have on your budget constraint if your $240 weekly take-home pay didn’t change at all over the same two-year period? Draw both budget constraints on the same set of axes. What if you were able to negotiate a raise to $360 per week? Draw this final budget constraint on the same set of axes as the first two. How does your final budget constraint compare with your original budget constraint from two years ago?
Question 25.7
3. You learned in the chapter that the process of utility maximization involves a comparison of marginal utilities per dollar, which are calculated as marginal utility divided by price. Consider two goods that most people consume at least some of during their lives: apples and cars.
If utility maximization was only about marginal utility (not marginal utility per dollar), which good (apples or cars) would consumers want to consume? Would they ever consume the other good?
If utility maximization was only about price (as opposed to marginal utility divided by price), which good (apples or cars) would consumers want to consume? Would they ever consume the other good?
Given your answers to parts a and b, and given the observation that some people eat apples and drive cars, explain why utility maximization involves a comparison of marginal utility divided by price, and not just one or the other.
Question 25.8
4. Fill in the blanks with either “good X” or “good Y,” where good X is measured on the x-axis and good Y is measured on the y-axis.
If the price ________ of is $8 and the price of is $12, then the price ratio (also the slope of the budget constraint) is 1.5.
A price ratio of 1.5 means that the consumer is able to trade 1 unit of _____ for 1.5 units of _____.
If another unit of ______ would give a consumer 20 extra units of utility, and another unit of _____ would give a consumer 10 extra units of utility, then the marginal rate of substitution for this consumer is equal to 2.
A marginal rate of substitution of 2 means that, from the consumer’s point of view, 1 more unit of ____ is as good as 2 more units of____.
If the price ratio is 1.5 and the marginal rate of substitution is 2, then the market values ___ more than the consumer does, and the consumer values ____ more than the market does. In this case, the consumer ought to buy less of ___ and more of ____.
Question 25.9
5. Suppose Haya has $120 of income left each week after she pays her bills and puts some money away in a savings account, and she has two ways to spend this extra money: go to the movies, which costs $18 including popcorn and a soda, or go out to a club with several friends, which costs $33 including the cover charge and drinks. Assuming these are her only two choices to spend the extra money, what can you say about the following bundles of going to the movies and clubbing? Which of these could possibly be the utility-maximizing bundle?
3 movies and 2 nights out at the club
2 movies and 3 nights out at the club
2 movies and 2 nights out at the club
Question 25.10
6. The utility-maximizing bundle of goods is found at the point of tangency between the budget constraint and an indifference curve. In the following diagram, the utility-maximizing bundle is the one labeled point K. There are two different, but equally important, ways to interpret this point.
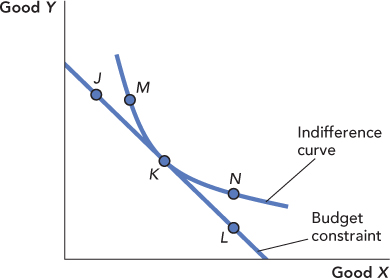
Of the three points on the consumer’s budget constraint (J, K, and L), what makes K special?
Page 486Of the three points on the consumer’s indifference curve (M, K, and N), what makes K special?
Question 25.11
7. Is marginal utility always diminishing? Consider playing cards. If playing cards were purchased one at a time, what would be true about the marginal utility of the 51st playing card compared with the marginal utility of the 52nd playing card? Why do you think it’s okay for economists to assume that marginal utility diminishes? How does the concept of marginal utility explain why playing cards are not sold individually, but only as entire 52-card decks?
THINKING AND PROBLEM SOLVING
Question 25.12
1. Suppose we wanted to investigate the saving and borrowing behavior of consumers. It’s not that difficult to extend our basic model. We can use the same framework as before, but define our two goods as “consumption in period 1” (horizontal axis) and “consumption in period 2” (vertical axis).
Construct a budget constraint for a consumer who earns $50 in income in period 1 and $150 of income in period 2. Label this point E for the “Endowment” point. Assume that he can choose to save some income in period 1 to be used in period 2, or to borrow some income from period 2 to use in period 1. (Let’s imagine the consumer saves the money by putting it in a piggy bank and can borrow money from his parents, who don’t charge interest.)
For the consumer in the situation just described, do you think he would consume at his endowment point or would he borrow or save?
Question 25.13
2. In Major League Baseball, teams in the American League use a designated hitter (DH) to bat in place of the pitcher, while teams in the National League require their pitchers to bat. Sports economists have noted that in the National League, batters are hit by pitches 15% less often than in the American League. Can you use the concepts from this chapter to explain this behavior from the point of view of the pitcher’s utility-maximizing decision about whether to throw pitches high and inside (where they are more likely to hit the batter)?
Question 25.14
3. Consider Facts and Tools question 2. Explain the income and substitution effects of the price changes on your optimal consumption bundle when the latte and scone prices increased, but your income did not.
Question 25.15
4. With inferior goods (like ramen noodles), the income effect works in the opposite direction from the income effect discussed in the text. If a consumer feels richer, she would buy less of an inferior good. If she feels poorer, more.
Suppose that a consumer eats two different foods: potatoes and meat. Potatoes are inferior and meat is a luxury. Describe both the income and substitution effects on the consumer’s optimal choice of potatoes and meat if the price of potatoes were to rise. Put the two effects together. What can you conclude?
What if you knew for sure that the substitution effect dominated the income effect? What would happen to the consumer’s optimal choices for potatoes and meat?
What if instead you knew that the income effect dominated the substitution effect? What would happen in this case? Why is this result a bit unusual?
Question 25.16
5. eMusic is a popular subscription MP3 Web site. For a monthly membership fee, you can download MP3s for a price that’s about half of what MP3s cost at iTunes or Amazon. Consider someone with $50 worth of income to spend on entertainment each month and who can choose to buy MP3s or “other stuff “—with a price equal to $1 per unit, so that other stuff is measured in dollars. Create budget constraints for each of the different eMusic membership plans. Prices have been rounded to make things simpler. (To simplify things, we’ll assume that the consumer will use his entire eMusic balance each month, even though eMusic members don’t have to do this. We’ll also just think about MP3 singles, not albums.)
No membership: The consumer has to purchase MP3s from another Web site, at $1 each.
eMusic Basic: For $12/month, the consumer gets 24 MP3 downloads. After that, the consumer would have to buy MP3s at another Web site for $1 each.
eMusic Plus: For $16/month, the consumer gets 34 MP3 downloads. After that, the consumer would have to buy MP3s at another Web site for $1 each.
Page 487eMusic Premium: For $21/month, the consumer gets 46 MP3 downloads. After that, the consumer would have to buy MP3s at another Web site for $1 each.
eMusic Fan: For $32/month, the consumer gets 73 MP3 downloads. After that, the consumer would have to buy MP3s at another Web site for $1 each.
Which plan do you think will be most popular? Which will be the least popular? Although eMusic has hundreds of thousands of members, most people are not members of eMusic. What must be true about their indifference curves? How many MP3s do these people download per month?
Question 25.17
6. In this chapter, we focused a lot on budget constraints, but time is an additional constraint that consumers face. Jackson has $40 per week to spend on leisure activities. He likes to bowl and to play racquetball. Bowling costs $4 per game, and a day pass to the racquet club costs $8. Jackson only has 7 hours of leisure time per week, and both bowling and racquetball each take 1 hour per game. Construct Jackson’s budget constraint and his time constraint on the same diagram. Consider each of the consumption bundles following that could possibly be Jackson’s utility-maximizing bundle. How does each of these bundles relate to Jackson’s two constraints?
Bowling twice per week and playing racquetball four times per week
Bowling four times per week and playing racquetball three times per week
Bowling six times per week and playing racquetball once per week
CHALLENGES
Question 25.18
1. This chapter argues that the ideal membership fee from Costco’s point of view would leave consumers indifferent between shopping at Costco and shopping elsewhere. Do you think most of the shoppers at Costco are indifferent? What prevents Costco from setting its ideal fee?
Question 25.19
2. Refer to Thinking and Problem Solving question 1. In that question, we assumed that the consumer earned $50 in period 1 and $150 in period 2, and that saving and borrowing were both interest-free. Let’s see if we can’t add even more real-life detail to this problem.
Draw a new budget constraint for the consumer if the period 1 income remains at $50, but the period 2 income falls to $100. Use the ideas of income and substitution effects to describe how this change would affect the optimal choice of the consumer.
Now let’s add another wrinkle: an interest rate. We’ll use the same endowment point from Thinking and Problem Solving question 1. Construct a budget constraint for a consumer that can earn 20% interest by saving money in period 1 for use in period 2, but also has to pay 20% interest to borrow money from period 2 for use in period 1. (These interest rates are high so that the impact is obvious on your graph; the results will still hold—although less dramatically—with lower interest rates.) What is the substitution effect of the addition of the interest rate? The income effect is more complicated, because it depends on the consumer’s preferences, which could be revealed by the pre-interest-rate behavior.
In December 2010, the average interest rate on money market and savings accounts was 0.7%, but the average rate on a variable-rate credit card was 14.4%. Obviously, the previous assumption that the interest rate is the same for borrowers and savers is not very realistic. Again, using more dramatic interest rates, can you construct a budget constraint for a consumer with the same initial endowment as previously who faces a 1% interest rate for saving and a 50% interest rate for borrowing? What do you notice about this budget constraint?
Question 25.20
3. Currently, if you join Disney’s movie club, you get 4 DVDs for $1 each, but you have to commit to buying at least 5 more DVDs at $20 each over the next year. Suppose the normal market price of a DVD is $16.
Construct two budget constraints: one for a consumer who joins Disney’s movie club and another for a consumer who doesn’t. Assume that both consumers have $112 worth of income. Place income on the vertical axis just as in Figure 25.12.
What kind of consumer is likely to get more utility from joining Disney’s movie club? What kind of consumer would not?
Page 488If Disney’s movie club wanted to charge an additional membership fee to generate more revenue, what would be the maximum it could charge for membership?
Question 25.21
4. Two special cases might result in indifference curves that look a little different from the ones discussed in the text.
If two goods are perfect substitutes, that means the consumer would always be willing to trade one for the other in a certain, fixed proportion. In this case, the MRS would be constant, which means that indifference curves would be straight lines. Suppose a consumer’s MRS between two goods X and Y is a constant 2.5, which means that the consumer is always willing to give up 1 unit of good X for 2.5 units of good Y. If the consumer has $180 in income to spend, the price of good X is $20 per unit, and the price of good Y is $10 per unit, what is this consumer’s utility-maximizing bundle of X and Y? Answer the question by thinking it through and then show with a diagram (including a budget constraint and an indifference curve) why your answer works.
If two goods are perfect complements, indifference curves have a very unusual shape. Let’s see if you can reason through this one. Consider left and right shoes. For most people, having left shoes alone (or right shoes alone) does not really provide any utility; rather, people get utility from having a pair of shoes that they can wear. In this case, left and right shoes are perfect 1:1 complements. Can you figure out what indifference curves would look like in such a case? To do this, it might be helpful to think about questions like the following: If someone has 4 right shoes and 4 (matching) left shoes, what’s the marginal utility of an extra right shoe? If a consumer had to compare the bundles (4 left shoes, 4 right shoes), (4 left shoes, 5 right shoes), and (7 left shoes, 4 left shoes), how would these bundles rank? Would any of these bundles be better than the others?
WORK IT OUT
Suppose we wanted to investigate the saving and borrowing behavior of consumers. It’s not that difficult to extend our basic model. We can use the same framework as before, but define our two goods as “consumption in period 1” (horizontal axis) and “consumption in period 2” (vertical axis).
Construct a budget constraint for a consumer who earns $100 in income in period 1 and $300 of income in period 2. Label this point E for the “Endowment” point. Assume that he can choose to save some income in period 1 to be used in period 2, or to borrow some income from period 2 to use in period 1. (Let’s imagine the consumer saves the money by putting it in a piggy bank and can borrow money from his parents, who don’t charge interest.)
For the consumer in the situation just described, do you think he would consume at his endowment point or would he borrow or save?