4.1 Scatterplots
Is it possible to predict a city’s average daily temperature based on its latitude? Do cities in the northern hemisphere at higher latitudes tend to have lower or higher average temperatures than cities at lower latitudes? Is there a relationship, in general, between average April temperatures and a city’s latitude? Table 4.1 displays data for 10 cities in the northern hemisphere.
| City | Latitude | Average April Temperature (°F) |
|---|---|---|
| Ithaca, NY | 42.440 N | 45 |
| Pensacola, FL | 30.467 N | 70 |
| Sacramento, CA | 38.517 N | 59 |
| Cayuga, Ontario | 42.803 N | 41 |
| Edmonton, Alberta | 53.300 N | 40 |
| Anchorage, Alaska | 61.167 N | 36 |
| Oaxaca, Mexico | 16.983 N | 72 |
| Panama City, Panama | 08.983 N | 84 |
| Dallas, TX | 32.818 N | 66 |
| Daneborg, Greenland | 74.300 N | 06 |
Source: www.weatherbase.com
Based on this small data set, we see a not-so-surprising fact: Cities closer to the equator tend to have warmer average April temperatures than cities closer to the North Pole. Because this data set is small, it is pretty easy to see this type of trend solely by viewing the data table. But what if the table had measurements for lots of cities or if a pattern was not obvious? In either situation it is difficult to get a general sense of any relationship between latitude and temperature only by looking at the table. As we saw in Chapter 3, graphing data often gives a good portrait, and graphing allows us to see patterns and relationships when they exist.
4.1.1 Creating a Scatterplot
The appropriate graph to use in the latitude/temperature situation is called a scatterplot. A scatterplot is a graph used to display bivariate, quantitative data (in this case, latitude and temperature) when each variable is collected on the same set of individuals. One variable is placed on the horizontal (x) axis and the other is placed on the vertical (y) axis. Each individual has a measurement value for x and y. The individual’s information is plotted in the x-y plane as an ordered pair (x,y). As with every other graph that we have encountered so far, we want to make sure that we clearly label the variables and include units on the graph.
Recall that in Chapter 2 we studied explanatory and response variables. A response variable is the outcome that we are investigating and the explanatory variable is the variable that explains or predicts the values of the response variable. With bivariate quantitative data, one of the two variables often is more sensibly the explanatory variable, while the other is the response variable. If this is the case, the explanatory variable is graphed on the horizontal axis and the response variable is graphed on the vertical axis.
To see how to create a scatterplot in the xy-plane, watch the StatTutor video Displaying relationships: scatterplots. (video pending)
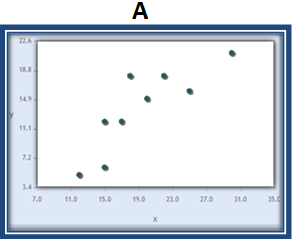
In practice, we usually let statistical software such as CrunchIt! construct the scatterplot. In our example, we are hoping to predict a city’s average April temperature based on its latitude. Therefore, with latitude as the explanatory variable and average April temperature as the response variable, we obtain the scatterplot shown in Figure 4.1.
Now Try This 4.1
The data set given here shows the number of hours per day spent on social network sites and the number of Facebook friends for a sample of statistics students at a university. Based on which variable is a more sensible choice as the explanatory variable and the response variable, choose the better scatterplot of the data.

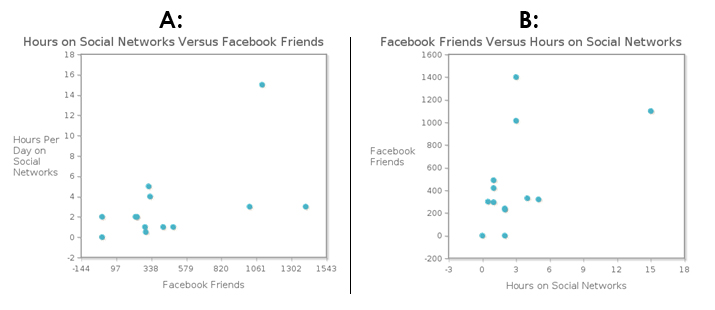
Which scatterplot (above) better represents the data set given?
| A. |
| B. |
4.1.2 Describing the Scatterplot
Once we’ve constructed the scatterplot, we look for a relationship between the variables. If we examine the scatterplot of temperature versus latitude (Figure 4.1), we see that there is a very clear association between these two variables. In such a setting, we attempt to describe the relationship we see in terms of its direction, form, and strength.
- Direction is positive if smaller values of x tend to correspond with smaller values of y and also if larger values of x tend to correspond with larger values of y. Similarly, direction is negative if smaller values of x tend to correspond with larger values of y and if larger values of y tend to correspond with smaller values of x.
- Form describes the general shape of the graph, typically linear or curved. The form is said to be linear if the graph of the data points comes close to falling on a line. Similarly, we call the form curved if the data points seem to lie near a curve. In this chapter, we’ll focus primarily on identifying linear trends.
- Strength refers to how much (or how little) scatter there is about the form. The relationship is said to be strong if there is very little scatter about the line (or curve). If there is a lot of scatter, we say that the relationship is weak. Arguably, in some cases, this is a subjective call.
To get a better sense of exactly what these terms are describing, let’s describe the direction, form, and strength of the association for the latitude-temperature plot. Here again is the scatterplot:
ADD FIGURE 4.1 HERE
- Direction: Because small latitude values tend to correspond with high temperature values and large latitude values tend to correspond with low temperatures, the direction is negative. Notice that we use the word "tend" to indicate that this relationship happens much more often than it does not.
- Form: Because the points cluster around a line, we say that the form is linear.
- Strength: Because most of the points in the plot are close to the line we visualize, we say that there is not much scatter in the form of the graph. Thus, we conclude that the strength of the relationship is strong.
In short, we conclude by saying that there is a strong, negative, linear association between latitude and temperature. Now you may be thinking that the strength was only moderate and not strong. Certainly, subjectivity comes into play when describing the strength of the association based on observing the scatterplot. What one person calls strong another may only consider to be moderate. In the next section, we will develop guidelines to help make this process more precise.
Figure 4.2 shows a scatterplot of the population of a city for various years between 1980 and 2005. A typical goal for local governments and city planners is to predict a city’s population for future years, so it is logical to regard population as the response variable and year as the explanatory variable.
We can see clearly that population is increasing over the time period from 1980 to 2005 so the direction is positive. The trend of the data seems to be curved and since there is very little scatter in the form of the graph, we say that the relationship is strong.
Now Try This 4.2
Explore your understanding of relationships between variables and characteristics of scatterplots.
Based on your knowledge of the variables described in (a) – (d), determine if the association is positive or negative.
(a) The number of miles on a Honda Civic’s odometer and its current value (in dollars):
(b) The height and weight of an adult female:
(c) The number of miles that a taxi-driver drives per week and his weekly gasoline bill:
(d) The number of absences a student has in a class during the semester and her grade on the final exam:
The following table gives HIV rates (% aged 15-49 with HIV) and fertility rates (number of children/woman) for twenty countries throughout the world. Does there appear to be an association between a country’s HIV rate and its fertility rate?
| Country | HIV Rate | Fertility Rate |
|---|---|---|
| Iceland | 0.2 | 2 |
| Australia | 0.1 | 1.8 |
| Canada | 0.3 | 1.5 |
| Switzerland | 0.4 | 1.4 |
| Spain | 0.6 | 1.3 |
| United States | 0.6 | 2 |
| Italy | 0.5 | 1.3 |
| Germany | 0.1 | 1.3 |
| Barbados | 1.5 | 1.5 |
| Poland | 0.1 | 1.3 |
| Costa Rica | 0.3 | 2.3 |
| Bahamas | 3.3 | 2.1 |
| Panama | 0.9 | 2.7 |
| Thailand | 1.4 | 1.8 |
| Iran | 0.2 | 2.1 |
| South Africa | 18.8 | 2.8 |
| Botswana | 24.1 | 3.2 |
| Niger | 1.1 | 5.8 |
| Venezuela | 0.7 | 2.7 |
| Belize | 2.5 | 3.4 |
Source: United Nations Development Programme
To see if there is an association between the two variables, we’ll use CrunchIt! to make a scatterplot of the data. Notice that in this situation there is not a clear choice for the explanatory variable (and thus the response variable). We will place fertility rate on the horizontal axis and HIV rate on the vertical axis. Figure 4.3 shows the result.
Based on the graph, it seems that there is a weak, positive, linear association between the two variables. An important feature of this data set is that it contains outliers, points whose x or y (or both) values are different from the rest. Niger is an outlier in the x-direction. The HIV rate in Niger is consistent with the other countries, yet its fertility rate (5.8 children/woman) is much higher than any of the other countries in the data set. South Africa and Botswana are both outliers in the y-direction because their HIV rates (18.8% and 24.1%) are much higher than those of the other countries.
In this case, the outliers, particularly those in the y-direction, affect the strength of the linear association. Without these outliers, the linear association would appear stronger. The presence of the outliers draws our eyes upward, away from the more linear appearance of the remainder of the points.
Now Try This 4.4
The graph below is the scatterplot of the data set that you investigated previously of hours spent on social network sites and number of Facebook friends. Determine the direction, form, and strength of the relationship displayed, and determine whether there are any outliers.
The direction of the relationship is . The form of the relationship is . The strength of the relationship is .
Does the scatterplot indicate any outliers? .
Many sets of bivariate data that we encounter in our daily lives are either strongly positive or strongly negative. For instance there is a strong, positive, linear relationship between the number of flights you take and the number of frequent flier miles that you’ve accumulated in a year. Likewise there is a strong, negative, linear association between the outside winter temperature and your monthly heating bill.
If we have data that display a fairly strong positive (or fairly strong negative) linear association, then a natural next step is to find an equation to model the data. This model can then be used to make predictions. For instance, knowing (based on the ten cities in Table 4.1) that there is a strong negative linear trend between latitude and temperature, we would like to find an equation that relates latitude to temperature. Why? Because then we can use the model to predict the average April temperature for cities not in our collected data set. For example, we could use the model to predict (with pretty good accuracy) the average April temperature for Toronto, Canada whose latitude is 43.667 N.
We’ll explore this idea in much greater detail in Section 4.3, but before doing so we need to consider a less subjective way to describe the strength and direction of the linear association between two quantitative variables. In Section 4.2, we will develop a numerical measure of such an association.