3.1 Graphical Data Descriptions
When we describe a set of data like our movie data, we do so by focusing on individual variables. Sometimes our variables are categorical (such as genre); sometimes they are quantitative (such as running time). The type of graph that we use to describe a variable depends on what kind of variable we are describing.
3.1.1 Graphs of Categorical Variables: Bar Graphs
If the measurements we collect are categorical, we first organize them into a frequency distribution or a relative frequency distribution. A frequency distribution displays the counts (frequencies) of measurements falling in each category, while a relative frequency distribution shows the fraction or percent of measurements falling into each category. If we compile the MPAA ratings of the 25 top-grossing movies, we can organize the data into a table showing both frequencies (counts) and relative frequencies (as decimal fractions).
| Rating | Count | Relative Frequency |
|---|---|---|
| G | 3 | 0.12 |
| PG | 4 | 0.16 |
| PG13 | 17 | 0.68 |
| R | 1 | 0.04 |
A bar graph is the simplest way to display categorical data, and can be used with frequency or relative frequency distributions for any categorical variable. A bar graph uses the heights of bars to indicate the count or relative frequency of measurements that fall into each category. In this case, the heights of the bars indicate the number of movies of each rating in the list of top-25 grossing movies in the United States.
Click here to see the relative frequency bar graph for the movie ratings. Notice that the relative sizes of the bars remain the same, while the scale on the vertical axis changes.
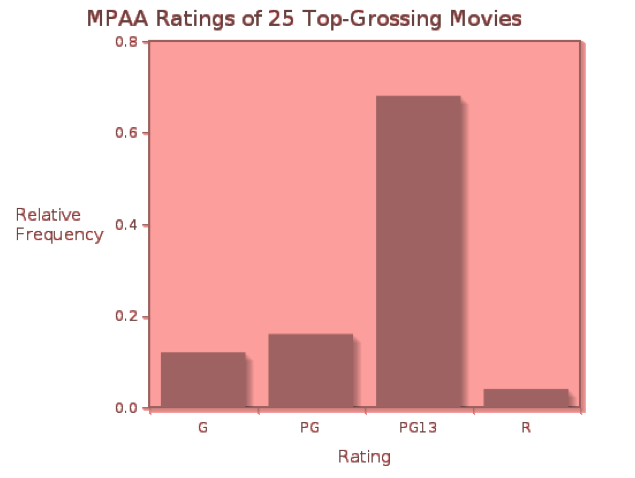
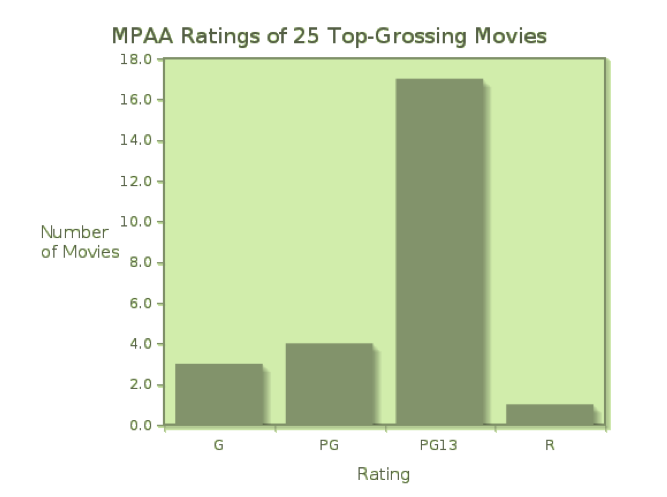
Because the rating data are simple, we probably get a “picture” of this distribution just from the frequency table. However, when there are more categories, a bar graph is a convenient way to visualize the distribution of measurements.
Consider the following data on the average daily consumption of various types of drinks by Americans in the year 2002:
| Type of Drink | Number of 8-ounce servings |
|---|---|
| Filtered or non-filtered tap water | 3.6 |
| Coffee | 1.8 |
| Soft drinks | 1.9 |
| Milk | 1.2 |
| Juice | 1.1 |
| Tea | 0.9 |
| Alcohol | 0.5 |
| Sport drinks | 0.2 |
Figure 3.2 displays these data.
A bar graph in which the categories are displayed in order of decreasing frequencies is called a Pareto Chart. Click here to see the Pareto Chart for What Americans Were Drinking in 2002.
What are the essential features of a bar graph that are displayed here?
- The graph has a title that describes the variable being categorized.
- Categories are displayed on the horizontal axis.
- Categories may appear in any order. They are displayed so that there are spaces between the bars, and each bar has an equal width.
- The frequencies (in this case, the number of ounces) or relative frequencies for the categories are displayed on the vertical axis.
- The vertical axis is marked off uniformly—equal numerical differences correspond to equal spaces on the axis.
Question 3.1
Americans spent $38.5 billion dollars on their pets in 2006, including spending in these categories:
| Expenditure | Billions of Dollars |
|---|---|
| Food | 15.4 |
| Supplies and Medicine | 9.3 |
| Veterinary Care | 9.2 |
Make a bar graph of this distribution. Compare your bar graph to the samples below:


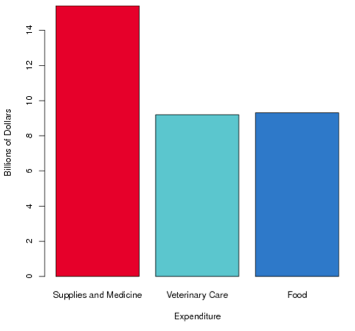
Which one of the graphs above does your graph most resemble?
| A. |
| B. |
| C. |
You are correct. The CrunchIt! bar graph for this distribution is Graph A, as shown below.

You did not select the correct graph. The CrunchIt! bar graph for this distribution is Graph A, as shown below.

Bar graphs are good vehicles for comparing the different values of a categorical variable, and are particularly useful when we want to compare these values over different time periods. In such a case, we can make side-by-side bar graphs, which show the count for each category in each time period.
Throughout the world, animal species are threatened by climate change, deforestation, and hunting. Some species have suffered more from such forces than others; Figure 3.1.5 shows the numbers of endangered species in 1996-1998 and 2006 for several types of animals.
| Numbers of Endangered Species | ||
|---|---|---|
| 1996-1998 | 2006 | |
| Mammals | 484 | 510 |
| Birds | 403 | 532 |
| Reptiles | 100 | 174 |
| Amphibians | 49 | 1180 |
| Fish | 291 | 491 |
In order to compare the number of endangered animals of various types between the years 1996-1998 and 2006, we can construct a side-by-side bar graph, as shown in Figure 3.1.3. From the bar graph, it is easy to see that the numbers of endangered species in all these categories has increased, with a phenomenal increase in the number of endangered amphibians over this time period.
Side-by-side bar graphs allow us to compare two or more distributions. In this case, we have distributions from two different time periods. In other settings, the distributions may come from two different populations or samples; for example, distributions of the types of college degrees awarded to males and to females could be displayed with a side-by-side bar graph.
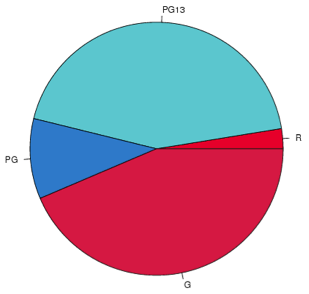
3.1.2 Graphs of Categorical Variables: Pie Charts
If the categorical data we have consist of all parts of a single whole, and each measurement falls into only one category, then we can also display the data in a pie chart. For the pet spending in the previous Try This! example, we can see that we do not have all parts of the whole. Americans’ pet spending in 2006 totaled $38.5 billion, but the spending on the three categories given totaled only $33.9 billion. Therefore, $4.6 billion were spent on other goods or services. If we wish to make a pie chart of these data, we can add an “Other” category to our table, and calculate the percentage of total expenditures that each category represents.
| Expenditure | Billions of Dollars | Percent of Total |
|---|---|---|
| Food | 15.4 | 40 |
| Supplies and Medicine | 9.3 | 24 |
| Veterinary Care | 9.2 | 24 |
| Other | 4.6 | 12 |
Figure 3.4 shows the pie chart for this distribution.
How does this pie chart compare to the bar graph? Does it provide additional information, or give us a better picture of the spending? Because we calculated the percent for “Other” expenditures, we have, in a sense, the whole picture of expenditures. It is easy to see that this “Other” category represents only half the spending of either veterinary care or supplies and medicine, while food is by far the largest expense.
If a pie chart is better, why don’t we use one all the time? The pie chart is appropriate only when we have frequencies or relative frequencies for all values of a single categorical variable. Neither is it appropriate when we are given data that represents averages calculated from a group of individuals, such as the “What Americans Are Drinking” displayed earlier in a bar graph.
The video StatClips: Summaries and Pictures for Categorical Data compares bar graphs and pie charts, and provides examples of each.

Question Sequence - Pie Charts
Question 3.2
The accompanying table shows the MPAA Ratings of the 25 Top-Grossing Movies (as of mid-November 2010).
| Rating | Frequency | Percent |
|---|---|---|
| G | 3 | 12 |
| PG | 4 | 16 |
| PG13 | 17 | 68 |
| R | 1 | 4 |
First, explain why it is appropriate to display these data in a pie chart.
3.1.3 Graphs of Quantitative Data: Histograms
If the data we collect are quantitative rather than categorical, a bit more analysis is required before we create a graph of the data. We have more choices to make when we graph quantitative data, and these choices depend on the characteristics of the data themselves. Are the data discrete or continuous? Is the range of the data large or small? Let’s begin by looking at a set of discrete data, with a small range.
Babe Ruth hit 714 home runs in his career; each home run was hit with 0, 1, 2, or 3 runners on base, as indicated in the accompanying table.
| Men on Base | Home Runs |
|---|---|
| 0 | 349 |
| 1 | 251 |
| 2 | 98 |
| 3 | 16 |
Using a bar to indicate the frequency of each number of men on base gives the accompanying histogram.
What are the essential features of a histogram that are displayed here?
- The graph has a title that describes the variable being analyzed.
- Values of the quantitative variable are displayed on the horizontal axis.
- The values appear on the horizontal axis in their natural numerical order, with each bar representing an interval of values of the variable. (Here each interval represents a single whole number.)
- Because each bar represents an interval of values, there are no spaces between the bars.
- Each measurement falls into only one interval.
- The counts for the intervals of values are displayed on the vertical axis.
- The vertical axis is marked off uniformly—equal numerical differences correspond to equal spaces on the axis.
Now let’s continue looking at some baseball data, but make things a little more complicated. The accompanying table gives the “winning percentage” for each American League baseball team at a certain point during a season. Even though this value is described as a “percentage,” it is really a decimal fraction of games won out of games played. These data are continuous, since this decimal fraction can be any value between 0 and 1, inclusive (though no team has either lost or won all of its games in a season).
| EAST | CENTRAL | WEST | |||
|---|---|---|---|---|---|
| Boston | .605 | Cleveland | .582 | Los Angeles | .593 |
| New York | .572 | Detroit | .544 | Seattle | .524 |
| Toronto | .497 | Minnesota | .493 | Oakland | .486 |
| Baltimore | .424 | Kansas City | .434 | Texas | .476 |
| Tampa Bay | .418 | Chicago | .425 | ||
The numbers in this data set range from a low of 0.418 to a high of 0.605. In order to “picture” them in a graph, we must decide on intervals by which to group them. These intervals are typically called “bins.” The trick in creating a good histogram is to find the bin width that is (as Goldilocks would say) “just right.” If the bin width is too small, very few measurements lie in each bin, and the histogram has many short, thin bars. If the bin width is too large, many measurements lie in each bin, and the histogram has only a few tall fat bars.
So let’s try some different widths, and display the resulting histograms. If we start our first bin and 0.400 and make the bin width 0.010, we get the histogram in Figure 3.6.
What we see here is the “too small” phenomenon. This is not a good picture of the distribution of team records, because many bins are empty (indicated by the spaces in the histogram), and most of the rest have only one measurement.
With the same starting point, 0.400, but a bin width of 0.075, we obtain Figure 3.7.
This is the “too big” phenomenon—not many boxes, and a similar number of values in each box. This is also not a good picture of the distribution of team records.
Finally, if we start our first bin at .400 and make the bin width .050, we get the histogram in Figure 3.8.
Perhaps not “just right,” but a pretty good picture of how the winning percentages are distributed. There are not a lot of empty bins (in fact, there are none here), nor are there just a few tall bins (the heights of the bars vary from 1 to 4). Would other bin widths work? Certainly. Is there a “magic” bin width that produces the “best” picture? Unfortunately not. Choosing a bin width requires practice. If you try several different bin widths, you will probably find a histogram that seems to give a good picture of your data. This is one of the situations in which statistics is more art than science.
It is important to note that we have to decide where we should display values that fall on a bin boundary, so that each measurement lies in only one bin. Because of our bin choices, none of the winning percentage data fell on a bin boundary. But it is common for this to happen. Each statistical software package handles this in a particular way, assigning a boundary value to either the bin to its left or the one to its right. While the choice may vary with your choice of software, each package handles boundary values in a consistent way. CrunchIt! counts a data value that falls on the boundary in the bin to its left; TI graphing calculators count such a value in the bin to its right.
Question 3.5
The accompanying table gives the average price per gallon of gasoline in the United States each month from 1999 through 2001.

Make a histogram of this data.
After you complete the histogram, click here and compare your histogram to the samples below:
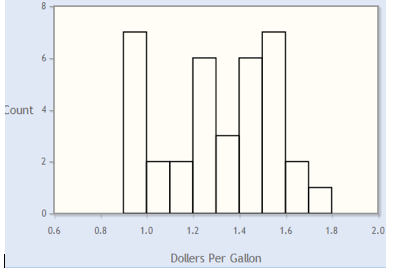
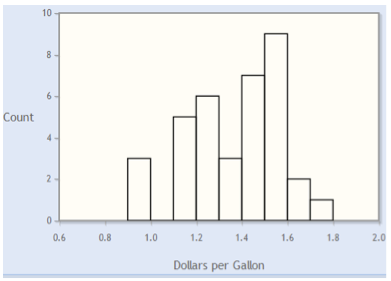
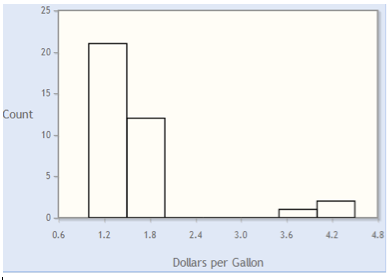
Which one of the histograms above does your histogram most resemble?
| A. |
| B. |
| C. |
Incorrect. The histogram below was created in CrunchIt! with bins starting at $0.90 and using a bin width of $0.10.

Does your choice of bin width yield a similar-looking histogram? If you have several empty bins, try a larger bin width. If you have fewer bins with many measurements in several of them, try a smaller bin width.
Correct. The histogram below was created in CrunchIt! with bins starting at $0.90 and using a bin width of $0.10.

Does your choice of bin width yield a similar-looking histogram? If you have several empty bins, try a larger bin width. If you have fewer bins with many measurements in several of them, try a smaller bin width.
3.1.4 Describing Histograms
Describing a histogram can give information about the distribution of data values even when the graph itself is not present. When we look at a histogram, we are interested in its shape, its center, the variability of the data (or sometimes referred to as the spread of the data), and whether there are any observations that seem unusual or separated from the rest of the data.
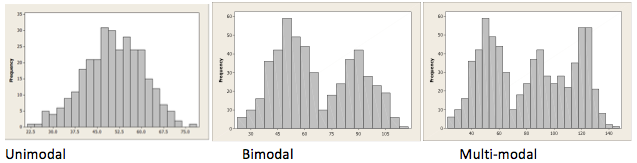
In terms of shape, we assess how many peaks the graph has, and how the graph falls away from these peaks. The peaks are the tall boxes in the histogram, and we call the histogram unimodal if there is one tall peak. The graph is bimodal if there are two non-adjacent tall peaks (of roughly equal height), and multi-modal if there are more than two such tall peaks. (These terms derive from the word mode, the measurement that occurs most frequently in the data set.)
If the graph can be divided in half so that the two halves are close to being mirror images, then we call the graph symmetric. If the peak of the graph occurs near the right-hand side, and the heights of the boxes decrease as we move to the left, we call the graph left-skewed. Similarly, if the peak of the graph occurs near the left-hand side, and the heights of the boxes decrease as we move to the right, we call the graph right-skewed.
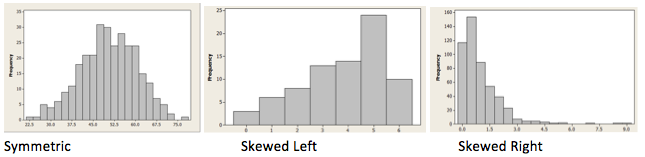
It is important to notice that, for statisticians, skewness describes not where the peak is, but rather the direction in which the graph “tails off.” This is different from (in fact, the opposite of) the way many people use the term “skewed” in every-day conversation.
In terms of center, we look for a value such that about half of the data falls below the value and half is above it. We use the heights of the boxes to determine what this value is.
To describe variability, we consider the minimum and maximum values as shown in the graph. We identify unusual data values as potential outliers if they seem outside the overall pattern of the graph. In order to be considered outliers, values should appear quite different from the rest of the data, not just separated by an interval or two from the others.
If we consider the histogram of gasoline prices that we created in CrunchIt! (shown here in Figure 3.11), we see that this distribution is unimodal, because it has one peak (occurring at the interval from 1.5 to less than 1.6). The distribution is left-skewed, because the graph falls away from this peak farther to the left than to the right.
To find the center, we look for the interval that contains the eighteenth or nineteenth measurements (in size order), because these are the middle measurements in this set of 36 observations. We consider the heights of the boxes, beginning on the left. While the scale is marked off using tenths, the number of months themselves are whole numbers. The first box is 3 units tall, the second one is 5 units tall, and the third one is 6 units tall. So the first three boxes represent the smallest 14 measurements. The fourth box is three units tall, so the fifteenth, sixteenth and seventeenth measurements lie in that interval. That means that the eighteenth and nineteenth measurements lie in the interval from 1.4 to less than 1.5. So we might say that the center of the distribution is about $1.45 (since these measurements are dollars and cents).
The data values range from 0.9 ($0.90) to 1.8 ($1.80). While there is a gap between the first and second boxes, the data represented by the first box are not unusual enough to be called outliers.
We should note that the choice of bin width can alter the shape of a histogram somewhat, so these verbal descriptions are not precise characterizations of the distribution’s shape, center, and variability. Further, two people looking at the same histogram may have different descriptions of the histogram, particularly in regard to its shape. More often than not, statistics requires an interpretation of results that may legitimately vary from person to person.
Consider the histogram in Figure 3.12, which displays the distribution of petal length (in centimeters) for a sample of Setosa iris.
The data used to create this histogram is part of a famous data set, published in 1935 by Edgar Anderson. The data set was used by the pioneering statistician R. A. Fisher to develop a model for distinguishing between several Iris species.
Is this distribution symmetric (two very similar “halves”) or slightly right-skewed (falling away from the peak farther to the right than to the left)? It depends entirely on your perspective. Such differences in interpretation happen frequently in statistics, a reality that is not necessarily comforting to a mathematics student trained to find a unique set of solutions to an algebraic equation. Ambiguity is a part of life, and a part of statistics as well. As you continue your study of statistics, keep an open mind about possible interpretations of your data, understanding that another individual may have chosen a different “best” interpretation. In this chapter we will also discuss numerical methods for describing data. These numerical measures can enhance our understanding of a distribution’s properties, even when they do not eliminate ambiguity.
3.1.5 Graphs of Quantitative Data: Stem and Leaf Plots
A stem and leaf plot is another graphical measure for displaying quantitative data. In a stem and leaf plot (often called a stem plot), each numerical value is broken into its “stem” and its “leaf.” The stem consists of all digits except the final digit; the leaf is the final digit. If we look at the average gas price data, and first round each value to the nearest cent, we get the data:
So for the first measurement, the stem would be “0.9” and the leaf would be “7.” Of course, the “7” is not the whole number 7, but rather .07, since the 7 occurs in the hundredths place of our decimal. Similarly, for the measurement 1.62, the stem would be “1.6,” and the leaf would be “2.”
We create a graph by putting all the stems to the left of a vertical line, and then placing each leaf in its appropriate row, producing the plot in Figure 3.14.
Notice that when we create a stem and leaf plot, we indicate all stems in order from the smallest to the largest, regardless of whether there are any leaves corresponding to that stem. In the plot above, the stem “10” has no leaves, because there are no gas prices between $1.00 and $1.09.
You can see that the stem and leaf plot looks very much like a histogram turned on its side. Thus, we can describe the shape, center, amount of variability in the distribution, and possible outliers for a stem and leaf plot in the same fashion as we did for a histogram. All that is required is that we rotate the plot so that the stems are in numerical order from left to right, with the leaves stacked vertically above their stems.
Figure 3.1.19 shows the stem plot for the gas price data rotated in this fashion, along with a histogram of the same data. Based on this plot, we can see that the distribution of gas prices is skewed to the left. The center of the distribution is about $1.44, and that gas prices range from $0.96 to $1.73.
Does a stem and leaf plot provide information that a histogram does not? In a histogram, once you create the graph, the data values are “gone”—they do not appear in the graph. On the other hand, in a stem and leaf plot, the data values used to construct the graph can be seen in the graph. Despite this useful feature, you will find that histograms are used more often than stem and leaf plots, particularly when data sets are quite large.
The video Snapshots: Visualizing Quantitative Data shows statisticians using stem and leaf plots and histograms to get a picture of research data.

Question 3.6
The heights in inches of 25 randomly selected adult females in the United States are shown in the table below.
| 63.1 | 61.1 | 62.6 | 64.1 | 63.8 | 63.7 | 62.9 | 65.5 | 68.2 | 64.1 |
| 62.9 | 60.8 | 66.9 | 69.6 | 62.9 | 61.8 | 62.9 | 66.0 | 64.9 | 63.7 |
| 61.4 | 63.4 | 66.8 | 65.4 | 70.2 |
(a) Make a stem and leaf plot of these data.
(b) Describe the shape, center, and variability of this distribution.
(a) The stem and leaf plot is shown below:
(b) This distribution is skewed to the right. The center of the distribution is the 13th measurement, which is 63.7 inches. The data ranges from 60.8 to 70.2 inches so there is a fair amount of variability in female heights.
When graphing a large data set, it is sometimes useful to “split” the stems to avoid having leaves with long strings of stems. Each stem then appears twice in the plot, once in a row displaying leaves from 0 to 4, and a second time in a row displaying leaves from 5 to 9. This technique corresponds to using more bins (and hence a smaller bin width) when making a histogram.
3.1.6 Graphs of Quantitative Data: Time Plots
The final graph that we consider is a time plot. A time plot shows how a quantitative variable changes over time. Typically, individual data points are plotted and then connected with either line segments or a smooth curve. Such plots are useful for displaying trends over a time period, particularly when investigating increases or decreases in a studied variable. The Bureau of Transportation Statistics reports the following numbers of cancelled flights over the calendar years 2000 to 2006:
| Year | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 |
|---|---|---|---|---|---|---|---|
| Number of Flights Cancelled | 24,515 | 19,891 | 7,301 | 8,341 | 17,611 | 25,084 | 9,787 |
Figure 3.16 shows a time plot for these data.
Question 3.7
Make a time plot for the data below, which show the percentage of U.S. Households saving for retirement in the indicated year.
| Year | Percent |
|---|---|
| 2000 | 78 |
| 2001 | 69 |
| 2002 | 72 |
| 2003 | 71 |
| 2004 | 68 |
| 2005 | 69 |
| 2006 | 70 |
| 2007 | 66 |
Use the graph to comment about the trend in retirement savings over this time period.
In general, the graph reflects a downward trend in the percentage of U.S. households saving for retirement. While the percentage fell from 28% in 2000 to 66% in 2007, there were increases in the percentage from 2001 to 2002, and again from 2004 to 2006.
3.1.7 Cautions about Making and Interpreting Graphs
Choosing the correct graph to display data is not always clear cut. Sometimes quantitative data are grouped in classes of unequal width; those data cannot be represented by a histogram. The data is then considered categorical, and a bar graph or pie chart must be used.
According to the Florida Department of Education, 105,977 students were enrolled in a developmental education or college preparatory course during 2006 – 2007. Figure 3.1.9 gives the distribution of those students by age.
| Age | Number of Students |
|---|---|
| 18 or younger | 21,877 |
| 19 - 21 | 42,115 |
| 22 - 35 | 31,003 |
| 36 or older | 10,982 |
Age is certainly a quantitative variable, but because the ages are grouped in unequal classes, we cannot use a histogram to display them. Because the data set is so large, a pie chart (Figure 3.17) is preferable to a bar graph.
When we looked at the data on Babe Ruth’s home runs by men on base, we treated the variable as quantitative, with whole number values 0, 1, 2, and 3. We constructed a histogram (Figure 3.5) to display the data. If we had considered the number of men on base as categories, we would have created the bar graph in Figure 3.18 rather than a histogram.
And because the categories “None, One, Two, Three” represent all the possibilities, we can also convert these data to percentages and display them in a pie chart (Figure 3.19).
| Men on Base | Home Runs | Percentage |
|---|---|---|
| None | 349 | 49 |
| One | 251 | 35 |
| Two | 98 | 14 |
| Three | 16 | 2 |
Do we get a different impression of Babe Ruth’s home runs when we use a histogram, a bar graph, or a pie chart? Probably not, so in this case any one of the graphs is acceptable.
When creating or interpreting a graph, it is important to pay attention to the graph’s axes. With a graph of an algebraic function, the axes are generally shown as the standard x- and y-axes (the lines y = 0 and x = 0). Real data can have values that are large enough that it is unreasonable to show all values beginning with 0. In such situations the axes should be clearly labeled (as in the CrunchIt! time plot in the answer above) to indicate actual data values near where the axes meet.
It is often particularly misleading when the vertical axis does not start at 0, because small changes in values can appear large when the scale is truncated. In the CrunchIt! time plot, the lowest percentage value is 66, while the highest is 78. The difference in these values seems exaggerated because the values from 0 to 66 do not appear on the axis. Figure 3.20 shows two time plots of the retirement savings data, one using the scale created automatically in CrunchIt!, and a second with a vertical axis starting at 0.
Do these two graphs give different impressions about how the percentage of households saving for retirement has changed? When you are creating a graph, try not to mislead your audience. When you are the viewer of a graph, think about how the data could have been presented differently.
A graph of a set of data can provide a good visual summary of important features of the data. In choosing an appropriate graph, you must first consider whether your data is categorical or quantitative.
Bar graphs and pie charts are used with data that is categorized. This includes not only data involving categorical variables (such as color or gender), but also quantitative data that has been sorted into unequal intervals.
Histograms, stem and leaf plots, and time plots are used with quantitative data. Histograms are commonly used to display frequencies or relative frequencies, and are used to approximate the shape, center and variability of the distribution. Like histograms, stem and leaf plots show the characteristics of the distribution, but they also retain the individual data values. They are best used with smaller data sets. Time plots display the changes in one or more quantitative variables over time.
In all use of graphical displays, the best advice is to keep the graph as simple as possible. While the media often display fancy graphs with 3-dimensional effects, statisticians prefer plain (if somewhat boring) 2-dimensional displays. Adding volume to boxes or pie segments distorts the proportions of the graph and can mislead the viewer. In all statistical presentations, giving an accurate picture of the data is the ultimate goal.