MAGNITUDE SCALES
Greek astronomers, from Hipparchus in the second century b.c.e to Ptolemy in the second century c.e., undertook the classification of stars strictly by evaluating how bright they appear to be relative to each other. This comparison made sense because back then astronomers assumed the stars were all at the same distance from us, and, therefore, differences in brightness due to different stellar distances from Earth were not expected. Classification regardless of distance is still useful to help us navigate around the night sky, and so we will study it now. In Section 10-
Distances to Nearby Stars
Recall from Discovery 2-
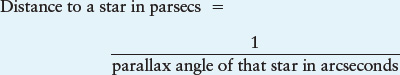
or
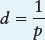
where d is the distance to the star and p is the parallax angle of that star.
The equation is only this simple in these units, which is one of the main reasons why many astronomers discuss cosmic distances in parsecs rather than light-
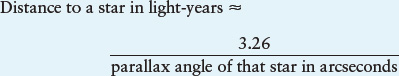
or
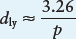
where dly is the distance to a star in light-
Example: The star nearest to the solar system, Proxima Centauri, has a parallax angle of 0.77 arcsec, and so its distance is 1/0.77, or approximately 1.3 pc. Equivalently, Proxima Centauri is 4.24 ly away. The parallax of Proxima Centauri is comparable to the angular diameter of a dime seen from a distance of 3 km. The parallax angles of the 25 nearest stars are listed in Appendix F: The Nearest Stars.
297
10-2 Apparent magnitude measures the brightness of stars as seen from Earth
The brightnesses of stars measured without regard to their distances from Earth are called apparent magnitudes, denoted by lowercase m. The brightest stars were originally said to be of first magnitude, and their apparent magnitudes were designated m = +1. Those stars that appeared to be about half as bright as first-
More quantitative methods of classifying stars were developed in the mid-
Astronomers also extended the magnitude scale so that dimmer stars, visible only through telescopes, could be included in the magnitude system. For example, the dimmest stars visible through a pair of powerful binoculars have an apparent magnitude of about m = +10. Time-
298
Insight Into Science
Bigger Is Not Necessarily Brighter Numbering as well as naming schemes may be counterintuitive in science. You might expect brighter stars to have larger, more positive numbers than dimmer stars, but the apparent magnitude scheme is just the opposite. Similarly, we will see shortly that on the standard plot of stars used by astronomers, the Hertzsprung-
Knowing, as we now do, that stars are at different distances from us, the apparent magnitudes do not directly reveal fundamental stellar properties. All other things being equal, the closer of two identical stars appears brighter to us (has a smaller apparent magnitude) than the farther star. We take the different distances into account with either of two measures: absolute magnitude and luminosity.
10-3 Absolute magnitudes and luminosities do not depend on distance
To determine the total energy emitted by each star in space, astronomers need to take into account that different stars are at different distances from Earth. They do this by calculating the brightness each star would have if they were all at the same distance from here. Knowing how far away a star really is and how bright it appears (its apparent magnitude), we can calculate how bright it would be at any distance. Absolute magnitude, M, is the brightness each star would have at a distance of 10 pc (32.6 ly). Unfortunately, absolute magnitudes have the same counterintuitive numeric scale as apparent magnitudes.
Focus Question 10-2
What might cause the closer of two identical stars to appear dimmer than the farther one?
To understand the relationship between the apparent magnitude and the absolute magnitude, we need to know how the brightness of an object changes with distance. Suppose we observe two identical stars, one twice as far away as the other. How much dimmer will the farther one appear to be, as seen from Earth? Light moving outward from a source spreads over increasingly larger areas of space and, therefore, its brightness decreases with increasing distance. The inverse-
Imagine light moving out from a star (Figure 10-3a). Start with a small square area of light that has moved out a distance d = 1. The light in that square has a certain brightness. When the same square of light has gone twice as far (d = 2), you can see on the figure that it has become 4 times larger. The light in each of the same-
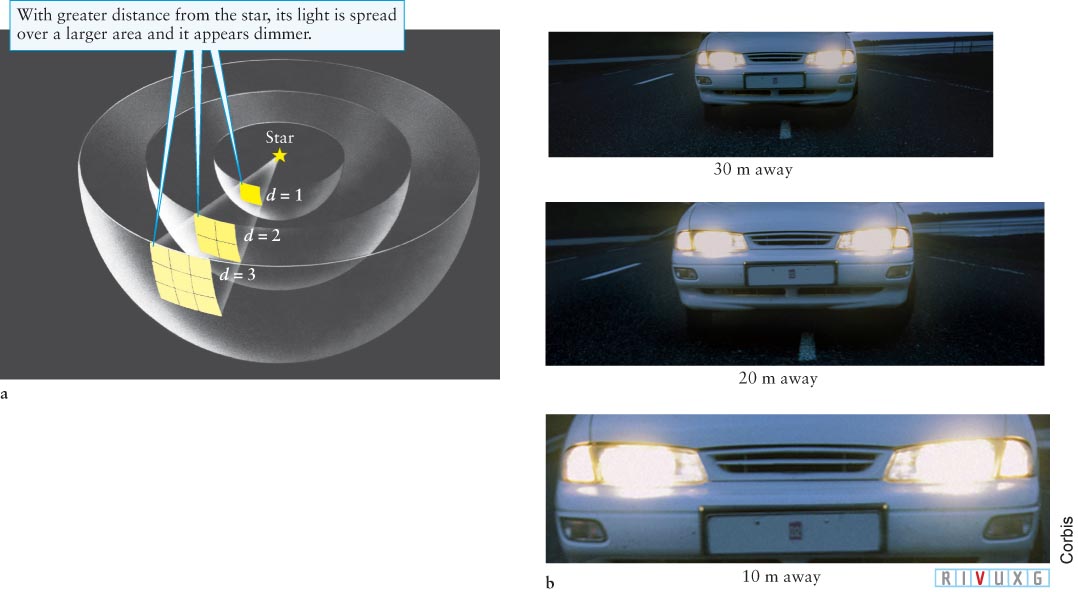
This inverse-
Apparent brightness decreases inversely with the square of the distance between the source and the observer.
Returning to our two identical stars, one twice as far away as the other, the farther one’s brightness decreases to 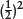 , or
, or  , of the brightness of its closer twin by the time the starlight gets to us.
, of the brightness of its closer twin by the time the starlight gets to us.
Absolute magnitudes are usually determined by calculations based on apparent magnitudes. Of course, we cannot just move a star to 10 pc distance and then remeasure its apparent magnitude. However, we can calculate the absolute magnitude of a nearby star: We first measure its apparent magnitude and then we find its distance by measuring its parallax angle. Combining these numbers, as shown in Discovery 10-2: The Distance–Magnitude Relationship, gives the star’s absolute magnitude.
Knowing the Sun’s true distance and its apparent magnitude, we can use the inverse-
 Because absolute magnitudes tell astronomers how bright stars are compared with one another, this information can be used to evaluate models of stellar evolution, which we discuss in the next few chapters. Absolute magnitudes range from roughly M = −10 for the brightest stars to M = +17 for the dimmest. Although absolute magnitudes give us comparisons between the energy outputs of stars, we also need to know the total energy they release. The total amount of electromagnetic power (energy emitted each second) is called a star’s luminosity. The greater the luminosity, the intrinsically brighter the star is compared to stars with lower luminosities. Therefore, the smaller or more negative a star’s absolute magnitude, the greater its luminosity. For convenience, stellar luminosities are expressed in multiples of the Sun’s luminosity, denoted L⊙. As we saw earlier, this value is about 3.83 × 1026 W. The intrinsically brightest stars (M = −10) have luminosities of 106 L⊙. In other words, each of these stars has the energy output of a million Suns. The dimmest stars (M = +17) have luminosities of 10−5 L⊙. We will provide both luminosity and absolute magnitude data about stars in the chapters that follow.
Because absolute magnitudes tell astronomers how bright stars are compared with one another, this information can be used to evaluate models of stellar evolution, which we discuss in the next few chapters. Absolute magnitudes range from roughly M = −10 for the brightest stars to M = +17 for the dimmest. Although absolute magnitudes give us comparisons between the energy outputs of stars, we also need to know the total energy they release. The total amount of electromagnetic power (energy emitted each second) is called a star’s luminosity. The greater the luminosity, the intrinsically brighter the star is compared to stars with lower luminosities. Therefore, the smaller or more negative a star’s absolute magnitude, the greater its luminosity. For convenience, stellar luminosities are expressed in multiples of the Sun’s luminosity, denoted L⊙. As we saw earlier, this value is about 3.83 × 1026 W. The intrinsically brightest stars (M = −10) have luminosities of 106 L⊙. In other words, each of these stars has the energy output of a million Suns. The dimmest stars (M = +17) have luminosities of 10−5 L⊙. We will provide both luminosity and absolute magnitude data about stars in the chapters that follow.
299
The Distance–Magnitude Relationship
The closer a star, the brighter it appears. The inverse-
M = m − 5 log (d/10)
where log stands for the base-
m − M = 5 log d − 5
Example: Consider Proxima Centauri, the nearest star to Earth (other than the Sun). By measuring its parallax angle, we know this star is at a distance from Earth of d = 1.3 pc. Its apparent magnitude is m = +11.1. Therefore, its absolute magnitude is
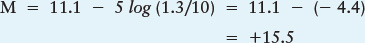
Compare! The Sun is an average star with M = +4.8, so Proxima Centauri is an intrinsically dim star. If you know any two of d, m, and M, you can calculate the third variable. For example, if we know a star’s absolute and apparent magnitudes, the equation can be used to determine its distance.
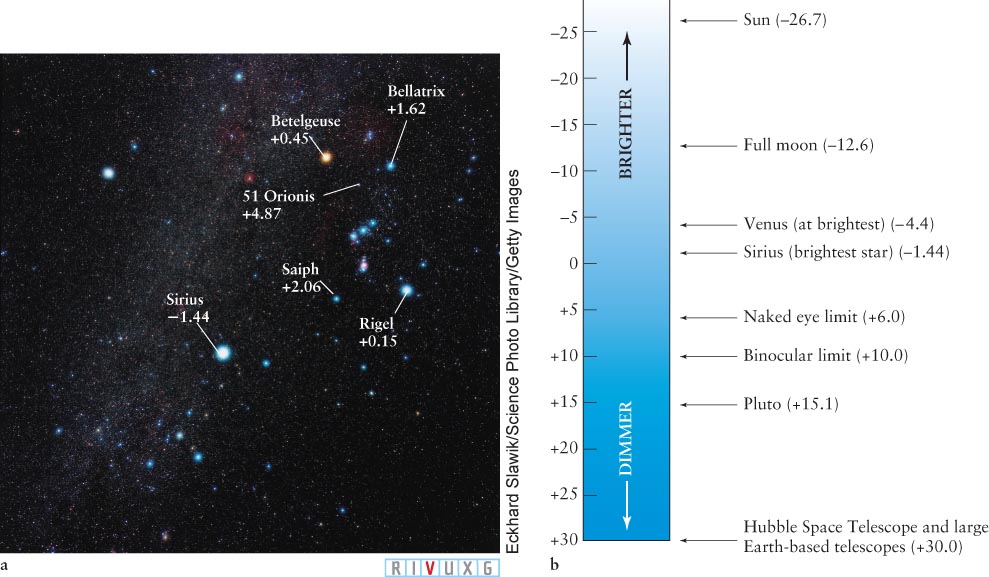
 Apparent Magnitude Scale (a) Several stars in and around the constellation Orion, labeled with their names and apparent magnitudes. (b) Astronomers denote the brightnesses of objects in the sky by their apparent magnitudes. Stars visible to the naked eye have magnitudes between m = −1.44 (Sirius) and about m = +6.0. However, CCD (charg
Apparent Magnitude Scale (a) Several stars in and around the constellation Orion, labeled with their names and apparent magnitudes. (b) Astronomers denote the brightnesses of objects in the sky by their apparent magnitudes. Stars visible to the naked eye have magnitudes between m = −1.44 (Sirius) and about m = +6.0. However, CCD (charg