Until Kepler’s time, astronomers had assumed that heavenly objects move in circles. For philosophical and aesthetic reasons, circles were considered the most perfect and most harmonious of all geometric shapes. However, using circular orbits failed to yield accurate predictions for the positions of the planets. For years, Kepler tried to find a shape for orbits that would fit Tycho’s observations of the planets’ positions against the background of distant stars. Finally, he began working with a geometric form called an ellipse.

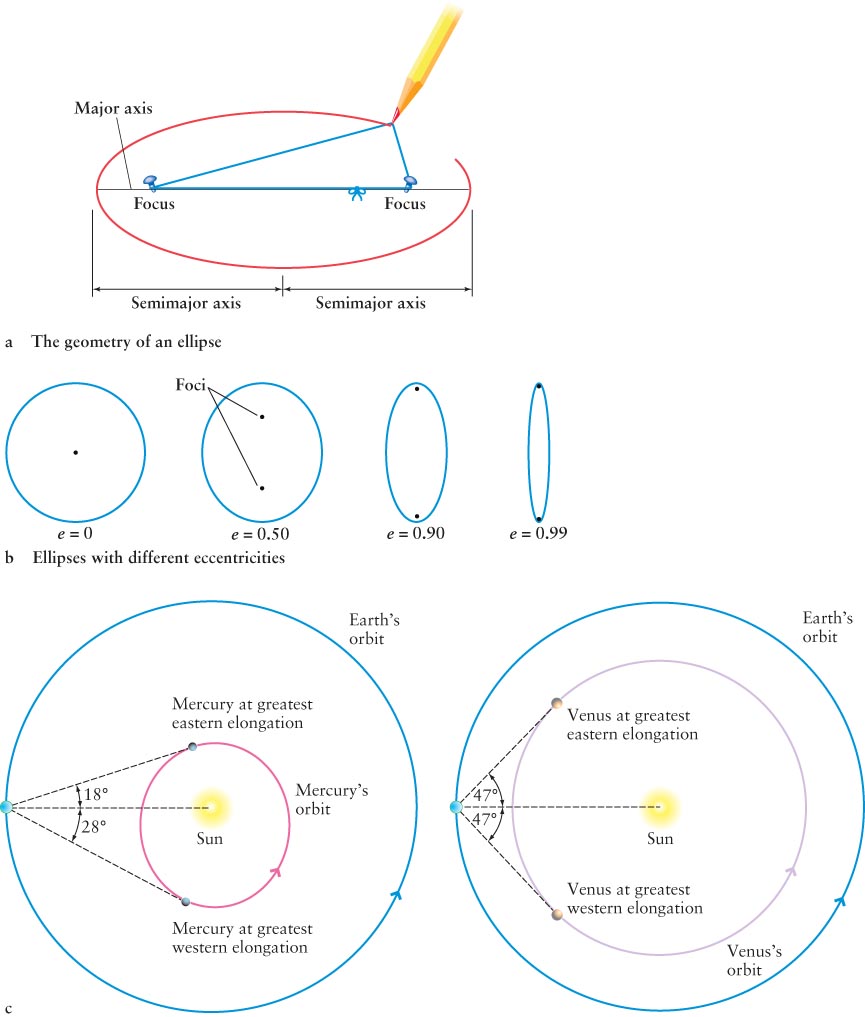
You can draw an ellipse as shown in Figure 2-8a. Each thumbtack is at a focus (plural foci). The longest diameter (major axis) across an ellipse passes through both foci. Half of that distance is called the semimajor axis. In astronomy, the length of the semimajor axis is also the average distance between a planet and the Sun.

To Kepler’s delight, the ellipse turned out to be the curve for which he had been searching. Predictions of the locations of planets based on elliptical paths were in very close agreement with where the planets actually were. Keep in mind that the following three laws that Kepler discovered merely quantified (gave equations for) observations that Tycho had made—Kepler did not have a theory to explain them. That would come nearly 80 years later with the work of Isaac Newton.

Kepler published his discovery of elliptical orbits in 1609 in a book known today as New Astronomy. This important discovery is now considered the first of Kepler’s laws:

The shapes of ellipses have two extremes. The roundest ellipse, occurring when the two foci merge, is a circle. The most elongated ellipse is nearly a straight line. The shape of a planet’s orbit around the Sun is described by its orbital eccentricity, designated by the letter e, which ranges from 0 (a circular orbit) to just under 1.0 (nearly a straight line). Figure 2-8b shows a sequence of ellipses and their associated eccentricities. Observations have revealed that there is no object at the second focus of each elliptical planetary orbit. Figure 2-8c shows the effect of orbital eccentricity. For example, the maximum elongation of Mercury (e = 0.21) seen from Earth varies by 10°, while the maximum elongation of Venus (e = 0.01) varies by less than 1°.

38

Tycho’s observations also showed Kepler that planets do not move at uniform speeds along their orbits. Rather, a planet moves fastest when it is nearest the Sun, a point on its orbit called perihelion. Conversely, a planet moves most slowly when it is farthest from the Sun, a point called its aphelion.

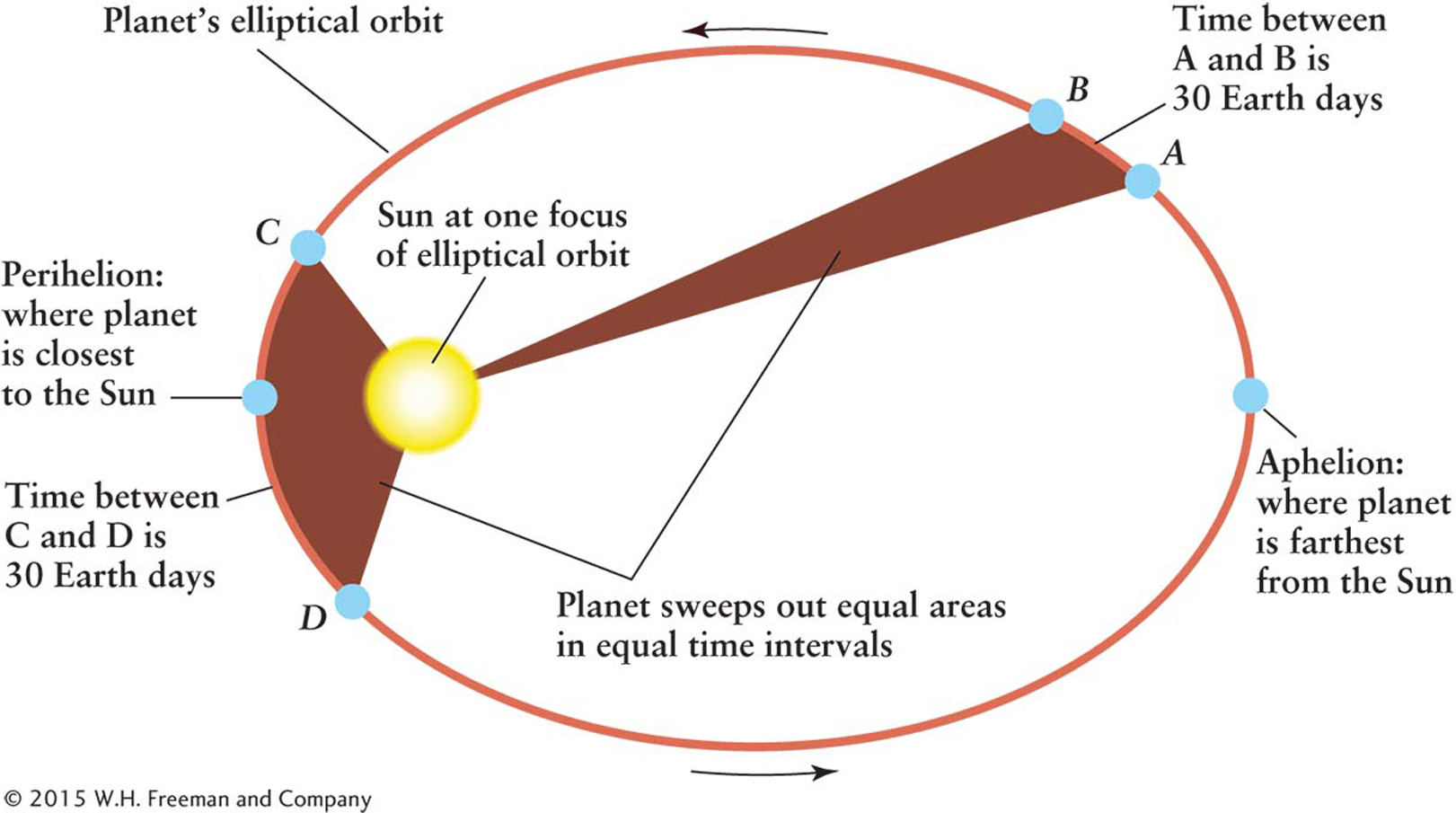
After much trial and error, Kepler discovered a way to describe how fast a planet moves anywhere along its orbit. This discovery, also published in New Astronomy, is illustrated in Figure 2-9. Suppose that it takes 30 days for a planet to go from point A to point B. During that time, the line joining the Sun and the planet sweeps out a nearly triangular area (shaded in Figure 2-9). Kepler discovered that the line joining the Sun and the planet sweeps out the same area during any other 30-day interval. In other words, if the planet also takes 30 days to go from point C to point D, then the two shaded segments in Figure 2-9 are equal in area. Kepler’s second law, also called the law of equal areas, can be stated thus:

39

A consequence of Kepler’s second law is that each planet’s speed decreases as it moves from perihelion to aphelion. The speed then increases as the planet moves from aphelion toward perihelion.

Kepler was also able to relate a planet’s year to its distance from the Sun. This discovery, published in 1619, is Kepler’s third law. This relationship predicts the planet’s sidereal period if we know the length of the semimajor axis of the planet’s orbit:

The relationship is easiest to use if we let P represent the sidereal period of an object’s orbit around the Sun in Earth years and a represent the length of its semimajor axis (that is, its average distance from the Sun) measured in astronomical units (AU). One astronomical unit is the average distance from Earth to the Sun; hence, a = 1 for Earth. The astronomical unit is used when measuring distances between objects in the solar system, because no powers of ten are needed, as they would be if these distances were referred to in kilometers or miles. (See Discovery 2-2: Units of Astronomical Distance for more details.) Now we can write Kepler’s third law for all objects orbiting the Sun as

P² = a³

This equation says that a planet closer to the Sun has a shorter year than does a planet farther from the Sun. Using this equation with Kepler’s second law reveals that planets closer to the Sun move more rapidly than those farther away. Using data from Table 2-1 and Table 2-2, we can demonstrate Kepler’s third law as shown in Table 2-3.

40

When Newton derived Kepler’s third law using the law of gravitation, discussed later in this chapter, he discovered that the mass of a planet affects the period of its orbit around the Sun. The mass of an object is a measure of the total number of particles of all different types that it contains and is expressed in units of kilograms. For example, the mass of the Sun is 2 × 10³⁰ kg, the mass of a hydrogen atom is 1.7 × 10^-27 kg, and the mass of the author of this book is 83 kg. At rest, the Sun, a hydrogen atom, and I have these same masses regardless of where we happen to be in the universe. It is important not to confuse the concept of mass with the concept of weight. Your weight is the force with which you push down on a scale due to the gravitational attraction of the world on which you stand.

41

However, the effect of the planet’s mass on the period of its orbit is exceedingly small for all the planets in the solar system, which is why the equation for Kepler’s third law, as shown in Table 2-3, gives such good results for the planets’ orbits even though it does not take their masses into account. When calculating the motion of pairs of stars orbiting each other, the effects of the masses must be included, as described in Discovery 10-3: Kepler’s Third Law and Stellar Masses.

Kepler’s three laws apply not only to the planets orbiting the Sun but also to any object orbiting another under the influence of their mutual gravitational attraction. Thus, Kepler’s laws apply to moons orbiting planets, artificial satellites orbiting Earth, and even (with the above caveat) two stars revolving around each other.

While Kepler was in central Europe working on the laws of planetary orbits, an Italian physicist was making dramatic observations in southern Europe. Galileo Galilei did not invent the telescope, but he was one of the first people to point the new device toward the sky and publish his observations. He saw things that no one had ever imagined—mountains on the Moon and spots on the Sun. He also discovered that like our Moon, Venus has phases from new to full and that the change in the apparent size of Venus as seen through his telescope was related to the planet’s phase (Figure 2-10). Venus appears smallest at full phase and largest at new phase. These observations were a big chink in the geocentric cosmology’s armor, as that model could not explain why Venus has a complete cycle of phases or changes size, while a heliocentric cosmology explains both. (Since Venus is always near the Sun in our sky, the geocentric model predicts that Venus should always have a crescent or quarter phase if it is closer to us than the Sun or a full or gibbous phase if it is farther away than the Sun—see Figure 2-10.) Galileo’s observations of a complete cycle of phases, therefore, supported the conclusion that Venus orbits the Sun, not Earth.

In 1610, Galileo also discovered four moons near Jupiter. Today, in honor of their discoverer, these are called the Galilean moons (or satellites, another term for moons). Galileo concluded that the moons orbit Jupiter because he saw them move in straight lines from one side of the planet to the other. (He did not see them move in elliptical orbits because from Earth we see their orbits from edge-on.) Confirming observations were made in 1620 (Figure 2-11). These observations all provided further evidence that Earth is not at the center of the universe. Like Earth in orbit around the Sun, Jupiter’s four moons obey Kepler’s third law: The square of a moon’s orbital period around Jupiter is directly proportional to the cube of its average distance from the planet.

Galileo’s telescopic observations constituted the first fundamentally new astronomical data since humans began recording what they saw in the sky. In contradiction to then-prevailing opinions, these discoveries strongly supported a heliocentric view of the universe. Because Galileo’s ideas could not be reconciled with certain passages in the Bible or with the writings of Aristotle and Plato, the Roman Catholic Church condemned him, and he was forced to spend his later years under house arrest “for vehement suspicion of heresy.” In 1992, Pope John Paul II stated that the Church erred in this condemnation.

42

A major stumbling block prevented seventeenth-century thinkers from accepting Kepler’s laws and Galileo’s conclusions about the heliocentric cosmology. Once anything on Earth is put in motion, it quickly comes to rest. So why don’t the planets orbiting the Sun stop, too?

The scientific method clarified most of the issues surrounding planetary orbits, leading to the equations and laws developed by the brilliant and eccentric scientist Isaac Newton (for example, he believed in alchemy). He was born on Christmas Day in 1642, less than a year after Galileo died. In the decades that followed, Newton revolutionized science more profoundly than any person before him and, in doing so, he found physical and mathematical evidence in support of the heliocentric cosmology.

Until the mid-seventeenth century, virtually all mathematical astronomy was done empirically. That is, astronomers from Ptolemy to Kepler created equations directly from data and observations.

Isaac Newton introduced a new approach. He began with three physical assumptions, now called Newton’s laws of motion, which led to equations that have since been tested and shown to be correct in many everyday situations. He also found a formula for the force of gravity (or gravitation), the attraction between all objects due to their masses. Putting the assumptions into mathematical form and combining them with the equation for gravity, Newton was able to derive Kepler’s three laws and use them to predict the orbits of bodies such as comets and other objects in the solar system. Newton also was able to use these same equations to predict the motions of bodies on and near Earth, such as the path of a projectile or the speed of a falling object.

If all of the external forces acting on an object do not cancel each other out, then there is a net external force acting on the object. Equivalently, we say that there is an unbalanced external force. For example, if you put a soccer ball between your hands and press on it so that it does not move, your hands represent a balanced pair of forces acting on the ball. In that case, you are exerting no net external force on the ball. Conversely, when your foot hits a soccer ball and the ball sails away, your foot has exerted a net external force on the ball.

At first, this law might seem to conflict with your everyday experience. For example, if you shove a chair, it does not move at a constant speed forever but comes to rest after sliding only a short distance. From Newton’s viewpoint, however, a “net external force” does indeed act on the moving chair—namely, friction between the chair’s legs and the floor. Without friction, the chair would continue in a straight path at a constant speed. A net external force changes the motion of an object.

43

Newton’s first law tells us why the planets keep moving in orbit around the Sun. First, they do not come to rest because there is virtually no air in space and hence no force from, for example, air friction opposing their motion. Second, they do not move in straight lines because there is an outside force acting on the planets to continually change their directions and keep them in orbit. As we shall see, that force is the Sun’s gravity.

Newton’s second law describes quantitatively how a force changes the motion of an object. To better appreciate the concepts of force and motion, we must first understand two related quantities: velocity and acceleration.

Imagine an object motionless in space. Push on it and it begins to move. At any moment, you can describe the object’s motion by specifying both its speed and direction. Speed and direction of motion together constitute an object’s velocity. If you continue to push on the object, its speed will increase—it will accelerate.

Acceleration is the rate at which velocity changes with time. Because velocity involves both speed and direction, a slowing down, a speeding up, and a change in direction are all forms of acceleration.

Suppose, for example, an object revolved around the Sun in a perfectly circular orbit. As this object moved along its orbit, its speed would remain constant, but its direction of motion would be continuously changing. This body would have acceleration that involved only a change of direction. In general:

In other words, the harder you push on something that can move, the faster it will accelerate. Also, an object of greater mass accelerates more slowly when acted on by a force than does an object of lesser mass acted on by the same force. That is why you can accelerate a child’s wagon faster than you can accelerate a car by pushing on them equally hard.

Newton’s second law can be succinctly stated as an equation. If a force acts on an object, the object will experience an acceleration such that

Force = mass × acceleration

Force is usually expressed in pounds or newtons. For example, the force with which I am pressing down on the ground is 814 newtons (183 lb). But I weigh 814 newtons only on Earth. I would weigh 136 newtons (30.5 lb) on the Moon, which has less mass and so pulls me down with less gravitational force. Orbiting in the International Space Station, my weight (measured by standing on a scale in the space station) would be 0, but my mass would be the same as when I am on Earth. Whenever we describe the properties of planets, stars, or galaxies, we speak of their masses, never of their weights.

Newton’s final assumption, called Newton’s third law, is the law of action and reaction.

For example, I weigh 183 lb on Earth, and so I press down on the floor with a force of 183 lb. Newton’s third law says that the floor is also pushing up against me with an equal force of 183 lb. (If it were less, I would fall through the floor, and if it were more, I would be lifted upward.) Even two objects that are not touching exert equal and opposite gravitational forces on each other. The Sun is exerting a force on each planet to keep it in orbit; hence, each planet exerts an equal and opposite force on the Sun. As each planet accelerates toward the Sun, the Sun in turn accelerates toward each planet.

Because the Sun is pulling on the planets, why don’t they fall onto it? Conservation of angular momentum provides the answer. Angular momentum is a measure of how much energy is stored in an object due to its rotation and revolution. The details of momentum are presented in Appendix P: Energy and Momentum. As the orbiting planets fall toward the Sun, their angular momentum provides them with motion perpendicular to that infall, meaning that the planets continually fall toward the Sun, but they continually miss it. Because their angular momentum is conserved, planets neither spiral into the Sun nor fly away from it. Angular momentum remains constant unless acted on by an external torque (also defined in Appendix P).

Angular momentum depends on three things: how fast an object rotates or revolves, how much mass it has, and how spread out that mass is. Consider, for example, a twirling ice skater. She rotates with a constant mass, practically free of outside forces. Because her angular momentum is therefore conserved, she can change how fast she is spinning by changing how spread out her mass is. According to conservation of angular momentum, as the spread of mass decreases, the rotation rate must increase. When she wishes to rotate more rapidly, she decreases the spread of her mass distribution by pulling her arms and outstretched leg in closer to her body (Figure 2-12). In astronomy, we encounter many instances of the same law, as giant objects, such as stars, contract.

44

We have now reconstructed the central relationships between matter and motion. Scientific explanation of the heliocentric cosmology still requires a force to hold the planets in orbit around the Sun and the moons in orbit around the planets. Newton identified that, too.

Isaac Newton did not invent the idea of gravity. An observant seventeenth-century person would understand that some force pulls things down to the ground. It was Newton, however, who gave us a quantitative description of the action of gravity, or gravitation, as it is more properly called. Using his first two laws, Newton showed mathematically that the force acting on each of the planets is directed toward the Sun. He expanded this result to the idea that the nature of the force pulling a falling apple straight down to the ground is the same as the nature of the force on the planets from the Sun. More generally, the gravitational force from every object acts to pull every other object directly toward it.

Newton succeeded in formulating a mathematical model that describes the behavior of the gravitational force that keeps the planets in their orbits (presented in Appendix R: Gravitational Force).

The inverse square part of this law means that gravitational force decreases with distance. Table 2-4 gives some examples of the inverse square law. Despite its weakening, the force of gravity from each object extends throughout the universe. Also, an object with twice the mass of another object exerts twice the gravitational force as the less massive object.

45

Using his law of gravity along with his three laws stated earlier, Newton found that he could mathematically explain Kepler’s three laws. For example, whereas Kepler discovered by trial and error that the period of orbit, P, and average distance between the Sun and planet, a, are related by P² = a³, Newton mathematically derived this equation (corrected by including a tiny contribution due to the mass of the planet, as mentioned earlier). Bodies in elliptical orbits are bound by the force of gravity to remain in orbit.

It seems plausible that astronauts floating in the International Space Station do not feel any force of gravity from Earth, but they do. Orbiting 330 km (approximately 200 mi) above Earth’s surface, they feel 90% as much gravitational force from the planet as we do standing on it. They are weightless, however, because as they fall earthward, their angular momentum carries them around the planet at just the right rate to continually miss it. The same effect occurs for all objects in orbit, as shown in the figure that opens this chapter.

Newton also discovered that some objects orbiting the Sun can follow nonelliptical paths. His equations led him to conclude that orbits can also be parabolas or hyperbolas (Figure 2-13). In both cases, such bodies would make only one pass close to the Sun and then travel out of the solar system, never to return. To date, all of the objects observed in the solar system began their existence in elliptical orbits, but some comets (small bodies of rock and ice) have received enough energy from being pulled by planets or from expelling jets of gas to develop parabolic or hyperbolic orbits.

Using the equations Newton derived, the orbits of the planets and their satellites could be calculated with unprecedented precision. Using his laws, mathematicians showed that Earth’s axis of rotation must precess because of the gravitational pull of the Moon and the Sun on Earth’s equatorial bulge (recall Figure 1-19). In the spirit of the scientific method, Newton’s laws and mathematical techniques were used to predict new phenomena. For example, Edmond Halley was intrigued by historical records of a comet that was sighted about every 76 years. Using his friend Newton’s methods, Halley worked out the details of the comet’s orbit and predicted its return in 1758. It was first sighted on Christmas night of that year, and to this day the comet bears Halley’s name (Figure 2-14).

Perhaps the most dramatic early use of the scientific method with Newton’s ideas was its role in the discovery of the eighth planet in our solar system. The seventh planet, Uranus, had been discovered by William Hersch in 1781 during a systematic telescopic survey of the sky. Fifty years later, however, it was clear that Uranus was not following the orbit predicted by Newton’s laws. Two mathematicians, John Couch Adams in England and Urbain-Jean-Joseph Leverrier in France, independently calculated that the deviations of Uranus from its predicted orbit could be explained by the gravitational pull of a then unknown, more distant planet. Each man predicted that the planet would be found at a certain location in the constellation of Aquarius in September 1846. A telescopic search on September 23, 1846, by German astronomer Johann Galle, revealed Neptune less than 1° from its calculated position. Although sighted with a telescope, Neptune was really discovered with pencil and paper.

46

It is a testament to Newton’s genius that his three laws were precisely the basic ideas needed to understand so much about the natural world. Newton’s process of deriving Kepler’s laws and the universal law of gravitation helped secure the scientific method as an invaluable tool in our process of understanding the universe. Figure 2-15 shows some of the effects of gravity at the scales of planets, stars, and galaxies.