We begin our study of why we see what we see with a familiar property of matter—temperature. We will discover that for many astronomical objects, their temperatures determine the relative numbers of photons that they emit at all different wavelengths.

Imagine that you have mounted an iron rod in a vise in a completely darkened room. You cannot see the rod because it emits too few visible photons, and you cannot feel its warmth without touching it because it is at the same temperature as the air in the room. Now imagine that there is also a propane torch in the room. You light it and heat the iron rod for several seconds, until it begins to glow. At the same time, you can feel the rod warm up, meaning that it is also emitting more infrared radiation.

The rod’s first visible color is red—it glows “red hot” (Figure 3-41a). Heated a little more, the rod appears orange and brighter and feels hotter (Figure 3-41b). Heated more, it appears yellow and brighter still and feels even hotter (Figure 3-41c). After even more heating, the rod appears white-hot and brighter yet. If it does not melt, further heating will make the rod appear blue and even brighter and feel even hotter. As confirmed by the photographs in Figure 3-41, this experiment shows how the amount of electromagnetic radiation that any object emits changes with its temperature. A “red-hot” object is the coolest of all glowing bodies.

If you were to put the light emitted by a heated object, like the iron rod, through a prism or diffraction grating (which separates the colors of light, just like a prism), you would discover that all wavelengths are present and that one is brightest. This peak wavelength is the color that the object appears to have. The experiment with the rod reveals two principles about the electromagnetic radiation emitted by objects as their temperatures change:

80

Most objects big enough to be seen with the naked eye continuously emit electromagnetic radiation as just described. The peak wavelength of any object’s radiation, that is, where it emits most intensely, is denoted λ_max. When the object is relatively cool, such as a rock or an animal, λ_max is a radio, microwave, or infrared wavelength. When it is hot enough, like a fire or the Sun, λ_max is in the range of visible light, giving a hot object its characteristic color. Exceptionally hot objects, such as some stars, emit λ_max in the ultraviolet part of the electromagnetic spectrum.

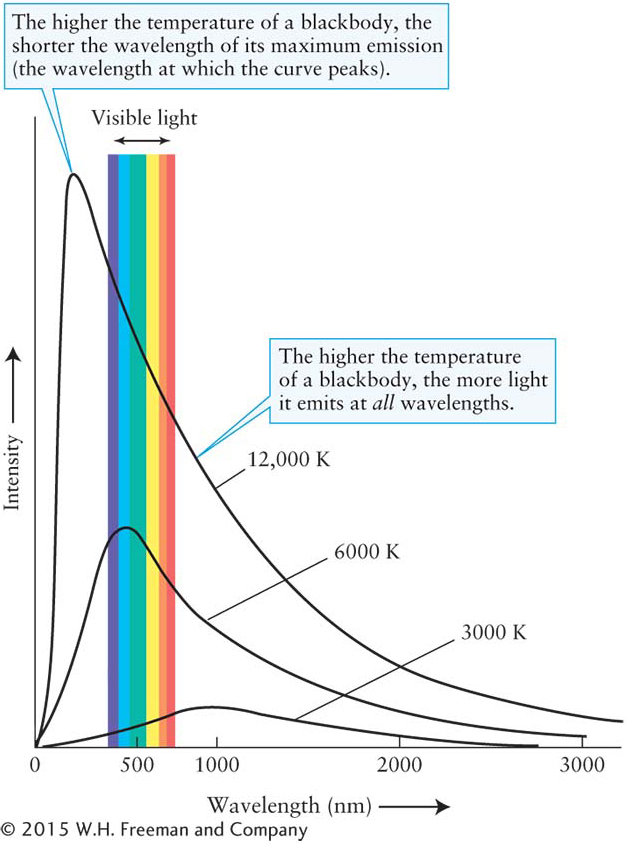
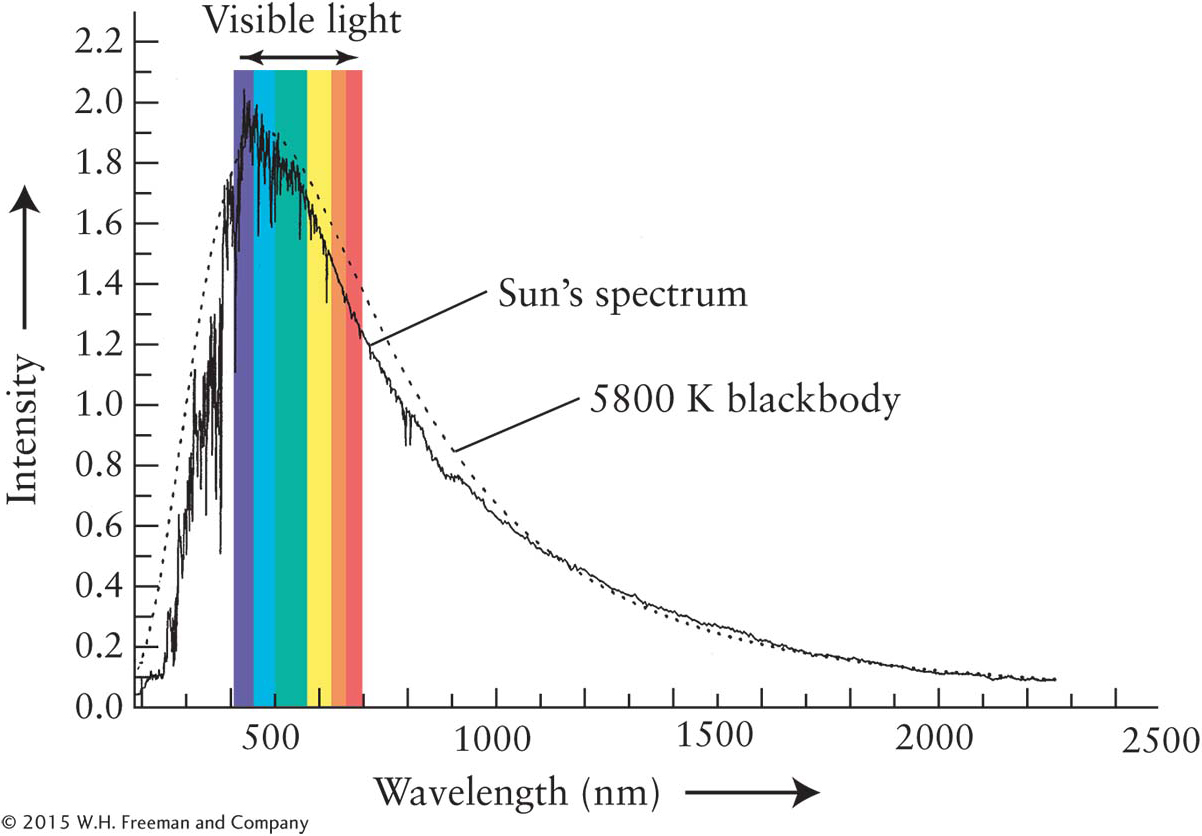
Stars, molten rock, and iron bars are approximations of an important class of objects that scientists call blackbodies. An ideal blackbody absorbs all of the electromagnetic radiation that strikes it. This incoming radiation heats up the blackbody, which then reemits the energy it has absorbed, but with different intensities at each wavelength than it received. Furthermore, the pattern of radiation emitted by blackbodies is independent of their chemical compositions. By measuring the intensity of radiation emitted by a blackbody at several wavelengths, it is possible to plot a curve of its emissions over all wavelengths (Figure 3-42). Ideal blackbodies have smooth blackbody curves, whereas objects that approximate blackbodies, such as the Sun, have more jagged curves whose variations from the ideal blackbody are caused by other physics (Figure 3-43).

81

The total amount of radiation emitted by a blackbody at each wavelength depends only on the object’s temperature and how much surface area it has. The bigger an object is, the brighter it is at all wavelengths. However, the relative amounts of different wavelengths (for example, the intensity of light at 750 nm compared to the intensity at 425 nm) depend on just the body’s temperature. So, by examining the relative intensities of an object’s blackbody curve, we are able to determine its temperature, regardless of how big or how far away it is. This process is analogous to how a thermometer tells your internal temperature no matter how big you are. (Temperatures throughout this book are expressed in kelvins. If you are not familiar with the Kelvin temperature scale, review Appendix B: Temperature Scales.)

Rather than absorb and reradiate light from an outside source like our iron rod, stars radiate electromagnetic radiation that is generated inside them. Even so, stars behave nearly like blackbodies, and the self-generated radiation they emit follows the idealized blackbody curves fairly well.

82

In 1893, the German physicist and 1911 Nobel laureate Wilhelm Wien showed that

In other words, the hotter any object becomes, the shorter is its λ_max, and vice versa. Wien’s law, often called Wien’s displacement law, is the mathematical relationship between the location of the peak for each curve in Figure 3-42 and that blackbody’s temperature.

Wien’s law proves very useful in computing the surface temperature of a star. It says that to determine that temperature, all we need to find is the peak wavelength of its electromagnetic radiation—we do not need to know the star’s size, distance, or any other physical property.

In 1879, the Austrian physicist Josef Stefan observed that

Think of the electric heating element on a stove. As this device becomes hotter, it gets brighter and emits more energy. Stefan’s result says that if you double the temperature of an object (for example, from 500 to 1000 K), the energy emitted each second from each piece of the object’s surface increases by a factor of 2⁴, or 16 times. If you triple the temperature (for example, from 500 to 1500 K), the rate at which energy is emitted increases by a factor of 3⁴, or 81 times. Stefan’s results were put on a firm theoretical foundation by Ludwig Boltzmann in 1885. In their honor, the intensity–temperature relationship for blackbodies is named the Stefan-Boltzmann law.

The Stefan-Boltzmann law and Wien’s law are powerful tools that describe two basic properties of blackbody radiation, namely, the relative rate at which photons of all different wavelengths are emitted and the wavelength that is emitted most intensely.

Blackbody curves, such as those shown in Figure 3-42, provide the same information as Wien’s law and the Stefan-Boltzmann law, as well as show the intensity of each blackbody at all wavelengths. Note that the blackbody curves for objects with different temperatures never touch or cross. Therefore, when astronomers measure the intensity of radiation from a star at a few wavelengths, they can determine the object’s temperature by fitting these measurements to the appropriate, unique blackbody curve.

Although intensity curves of stars closely “follow” blackbody curves, they are not ideal blackbodies. The differences between an ideal blackbody curve and the curves seen from actual stars reveal stellar chemistries, the presence of companion stars and planets too dim to see, and the motions of stars toward or away from us, among other information. We begin studying these issues by considering the actual spectrum of the Sun.

83

Figure 3-43 shows how the intensity of sunlight varies with wavelength. The blackbody curve for a body with a temperature of 5800 K is also plotted in this figure. Note how the observed intensity curve for the Sun nearly reproduces the ideal blackbody curve at most wavelengths. The differences in the two curves are due to photons removed from the Sun’s blackbody radiation by gases between the Sun’s visible surface and our eyes. We discuss this phenomenon further shortly. Because the observed intensity curves for most stars and the idealized blackbody curves are so closely correlated, the laws of blackbody radiation can be applied to starlight. The peak of the intensity curve for the Sun is at a wavelength of about 500 nm, which is in the blue-green part of the visible spectrum.

The shapes of ideal blackbody curves were first derived from basic physical principles (and a deeper understanding of matter and energy than was available to Ludwig Boltzmann) in 1900 by the German physicist Max Planck. To determine these curves, he had to assume that objects receive electromagnetic radiation as individual packets of energy. This surprising assumption was reinforced in 1905 by Albert Einstein, who suggested that light—a wave—also behaves as particles (photons), as discussed in Section 3-3. Planck was awarded the Nobel Prize in 1918 for his ideas about photons. Einstein’s 1921 Nobel Prize was for related work (he did not earn it for his development of special or general relativity, which we study in Chapter 12).

We can now describe our experiment with the iron bar at the beginning of this section in terms of the energies and intensities of photons. Recall from Section 3-3 that the energy carried by a photon is inversely proportional to its wavelength. In other words, long-wavelength photons, such as radio waves, carry little energy, while short-wavelength photons, like X-rays and gamma rays, each carry much more energy. When the rod was cool, it mostly emitted lower-energy infrared and radio photons; as it heated up, it emitted more and more photons of all wavelengths and therefore glowed more, eventually emitting mostly visible photons, which is why it looked brighter, felt hotter, and changed color.

The relationship between the intensity of electromagnetic radiation at every wavelength emitted by a given blackbody and its temperature is called Planck’s law (Table 3-1): Planck’s law gives the shapes of the curves in Figure 3-42. To summarize: A cool object emits primarily long-wavelength photons that carry little energy, while a hot object emits mostly short-wavelength photons that carry much more energy. Furthermore, hotter objects emit more photons of all wavelengths than do cooler objects and, according to Wien’s law, the hotter a blackbody, the shorter the wavelength of the peak of its emission. In later chapters, we will find these relationships invaluable for understanding how stars of various temperatures interact with gas and dust in space.

Note: > means greater than; < means less than

*1 eV (electron volt) = 1.6 × 10⁻¹⁹ J

**Microwaves, listed here separately, are often classified as radio waves or infrared radiation.

84