An atom is the smallest particle of a chemical element that still has the properties of that element. At the time of Kirchhoff’s discoveries, scientists knew that all matter is composed of atoms, but they did not know how atoms were structured. Furthermore, scientists saw that atoms of a gas somehow extract light of specific wavelengths from continuum spectra that pass through the gas, leaving dark absorption lines, and they perceived that the atoms then radiate light of precisely the same wavelengths—the bright emission lines (see Figure 3-46). But traditional theories of electromagnetism could not explain these phenomena. The answer came early in the twentieth century with the development of nuclear physics and quantum mechanics.

The internal structure of atoms first came into focus in 1908 when New Zealand native and 1908 Nobel laureate Ernest Rutherford and his colleagues at the University of Manchester in England were investigating radioactivity. They were expanding on work done earlier by Polish physicist (and double Nobel laureate, 1903 and 1911) Marie Curie, among others. Over time, a radioactive element naturally and spontaneously transforms into another element by emitting particles. Certain radioactive elements, such as uranium and radium, were known to emit particles moving with considerable speed. It seemed plausible that a beam of these high-speed particles would penetrate a thin sheet of gold. Rutherford and his associates found that almost all of the particles did pass through the gold sheet with little or no deflection. To their surprise, however, an occasional particle bounced back (Figure 3-50). It must have struck something very dense indeed.

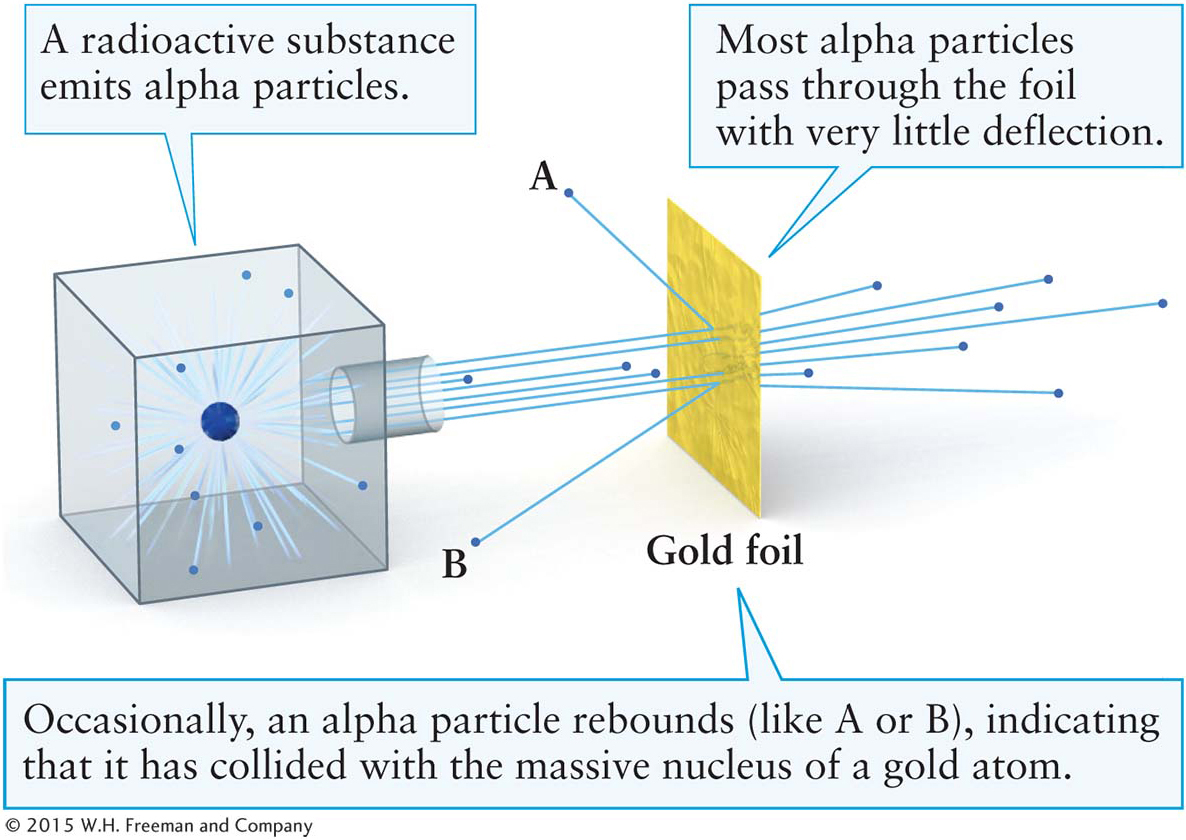
Within a few decades, the structure of atoms became evident. That dense “something” is now called the nucleus of the atom, and it consists of particles called protons and neutrons. Surrounding the nucleus, one or more electrons normally orbit. Newton’s second law (see Section 2-7) explains that electrons move much more than the nuclei they orbit because the electrons have only 1/2000 the mass of a proton or neutron.

89

Unlike the planets, whose gravitational interaction keeps them orbiting the Sun, electrons orbit nuclei because electrons and protons have a property called electric charge. All protons have the exact same positive charge, while all electrons have a negative charge equal in strength to the proton’s charge. The terms positive and negative are arbitrary and just indicate that the charges are opposite to each other. Particles with opposite charges attract each other. Therefore, protons attract electrons, and it is this attraction that keeps electrons in orbit around nuclei. The interaction between charged particles is a result of the electromagnetic force, the second of four fundamental forces in nature. (Gravitation is the first fundamental force we have discussed.)

Particles with the same type of charge, such as a pair of protons or a pair of electrons, repel each other. For atoms that have more than one proton in their nuclei (and many do), the protons are pushing away from each other. For nuclei to have more than one proton, there must be an attractive force stronger than the repulsion of protons to keep them glued together. The electrically neutral neutrons in the nucleus help provide that attractive force, called the strong nuclear force. This is the third of the four fundamental forces.

Many scientists find it fascinating that all of the interactions between matter and energy in nature occur as a result of just four forces, the above three plus the weak nuclear force. The weak nuclear force is involved in some radioactive decays, such as when a neutron transforms into a proton. In Chapter 14, we will further explore the weak nuclear force in our study of the evolution of the whole universe. The properties of all four fundamental forces are summarized in Table 3-2.

The number of protons in an atom’s nucleus, called the atomic number, determines the element of that atom. All hydrogen nuclei have 1 proton, all helium nuclei have 2 protons, all carbon nuclei have 6 protons, and so forth. There are 92 different types of elements that form naturally. Uranium is the most massive, with 92 protons (see Appendix N: Periodic Table of the Elements). As we will explore in Chapter 12, the fact that neutrons can transform into protons by emitting an electron and that protons can transform into neutrons by absorbing an electron is vital for the formation of elements with more than 26 protons.

In contrast to each atom of a given element always having the same number of protons in its nucleus, the nuclei of most elements can have different numbers of neutrons. For example, hydrogen, with 1 proton, can have 0, 1, or 2 neutrons; oxygen, with 8 protons, can have 8, 9, or 10 neutrons. Each different combination of protons and neutrons is called an isotope. There are three isotopes of hydrogen and three isotopes of oxygen. Hydrogen with no neutrons is the most common hydrogen isotope, while oxygen with 8 neutrons is by far the most abundant isotope of oxygen.

Some isotopes are stable, meaning that the numbers of protons and neutrons in their nuclei do not change. However, many elements have isotopes that are unstable and come apart spontaneously. These isotopes are radioactive, as discussed earlier in this section. For example, carbon with 6 neutrons, ¹²C (“carbon twelve”), is stable, while carbon with 8 neutrons, ¹⁴C (“carbon fourteen”), is unstable. ¹⁴C decays into nitrogen with 7 neutrons, ¹⁴N. Using radioactive age-dating techniques (see Appendix Q: Radioactivity and the Ages of Objects) on the oldest rocks brought back from the Moon, astronomers are able to determine roughly when the Moon formed (4.5 billion years ago). Applying the same technique to space debris found on Earth (meteorites), we can determine that the solar system, consisting of the Sun and everything orbiting it, formed some 4.57 billion years ago.

90

The number of electrons that orbit an atom is normally equal to the number of protons in its nucleus, thus making the atom electrically neutral. Astronomers denote neutral atoms by writing the atomic symbol followed by the Roman numeral I. For example, neutral hydrogen is written as H I and neutral iron is Fe I.

When an atom contains a different number of electrons than protons, the atom is called an ion. The process of creating an ion is called ionization. Ions are denoted by the atomic symbol followed by a Roman numeral that is one greater than the number of missing electrons. Positively ionized hydrogen (missing its one electron) is denoted H II, while positively ionized iron with seven electrons missing is denoted Fe VIII. Negative ions also exist, in which nuclei have more electrons orbiting than they have protons.

Atoms can share electrons and, by doing so, become bound together. Such groups of atoms are called molecules. Molecules are the essential building blocks of all complex structures, including life.

Because protons and neutrons have masses about 2000 times greater than the mass of an electron, over 99.95% of the mass of any atom is concentrated in its nucleus. The electron orbits are far from the nucleus, typically 10,000 times farther away than the radius of the nucleus. This immense distance is why you may have heard the statement that matter is mostly empty space.

Be careful not to imagine electrons as miniature planets orbiting the nucleus as a “miniature Sun.” Protons, neutrons, and electrons are not tiny solid bodies. Rather, like photons, they all have both wave and particle properties. The science that accurately describes their complex behavior is called quantum mechanics.

Quantum mechanics explains that electrons in atoms can exist in only certain allowed orbits around their nuclei, except when they are making a transition from one allowed orbit to another. These orbital conditions are completely unlike planets, which can exist at any distance (in any orbit) around the Sun. Each allowed electron orbit has a well-defined energy associated with it, and every different type of atom and molecule has a unique set of allowed orbits. These orbits and the transitions between them are the key to understanding the spectra that we have been discussing.

Consider an atom of the simplest hydrogen isotope, which contains just a single proton in its nucleus orbited by one electron. (This discussion generalizes directly to all of the other atoms and isotopes, made more complex only because they have more than one electron in orbit.) Figure 3-51 shows a hydrogen atom’s lowest energy levels.

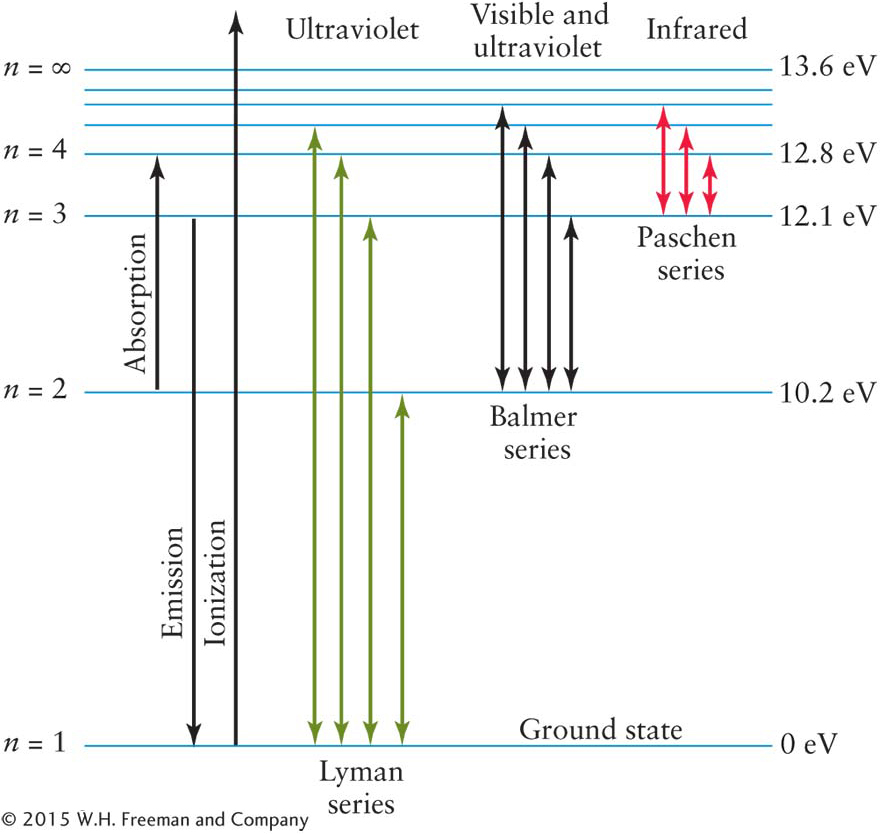
Normally, the hydrogen atom’s electron is in the lowest-energy allowed orbit or energy level, commonly called the ground state; this is labeled n = 1 in Figure 3-51. Each allowed orbit with successively higher energy is labeled n = 2, n = 3, n = 4, and so on. When an electron is in an orbit with more energy than the lowest-energy state available to it, it is said to be in an excited state. Electrons change orbits by absorbing or emitting photons. When a photon is absorbed, it vanishes and its energy becomes energy of the electron. However, electrons in orbit cannot absorb just any photon that they encounter. Electrons can absorb only those photons with energies exactly enough to boost them up to a higher-energy allowed orbit or with enough energy to completely remove them from orbit, an event called photoionization. Put another way, the nonionizing photons that are absorbed by electrons in atoms are those photons with energies equal to the difference between the energies of two allowed orbits. All nonionizing photons that do not satisfy this condition pass straight through the atom. If the electron starts in its ground state, then it must get exactly the energy necessary to move it to an excited state. If it is already in an excited state, then by absorbing a photon, it must transition to a higher-energy excited state.

91

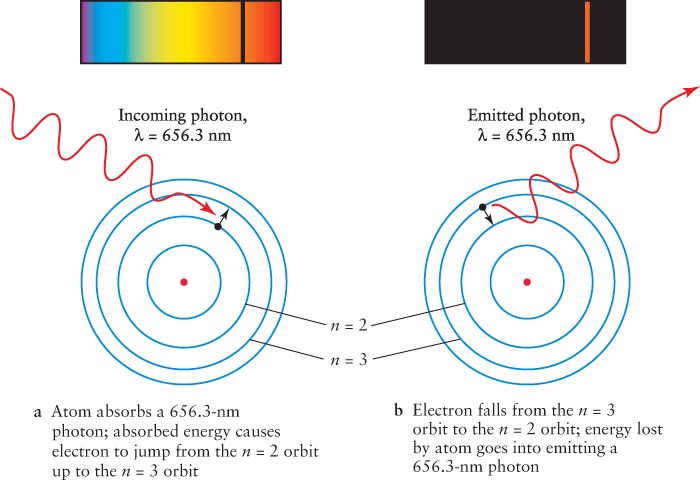
For example, referring to Figure 3-51 and Figure 3-52, transitions between the n = 2 and the n = 3 energy levels require the electron to absorb a photon with energy equal to 12.1 eV −10.2 eV = 1.9 eV (electron volt, a measure of energy). In this case, the photon absorbed by the electron has a wavelength of 656.3 nm (Figure 3-52a); it is a red photon (recall Figure 3-7).

Although some absorption occurs at optical wavelengths, it also happens in many other parts of the electromagnetic spectrum. Indeed, most of the transitions in hydrogen, shown in Figure 3-51 as the Lyman series (up from and down to n = 1) and the Paschen series (up from and down to n = 3), are nonvisible photons. Only a few of the Balmer series (up from and down to n = 2) transitions are visible, with the rest being ultraviolet. We will refer to Balmer transitions when we study stars. They are named after the Swiss physicist Johann Balmer, who first calculated their wavelengths in 1885. The longest-wavelength Balmer line is called H_α (H alpha), the second H_β (H beta), the third H_γ (H gamma), and so forth, ending with the shortest-wavelength Balmer line, H_∞ (H infinity). (The first dozen lines of the series have Greek-letter subscripts; those remaining are identified by numerical subscripts.) Part of the spectrum of a star having Balmer absorption lines H_α through H_ζ (H zeta) is shown in Figure 3-53.

An electron in an excited state of hydrogen is unstable. It loses energy by bumping into other particles and suddenly having either too much or too little energy than is necessary to be in that state. When this happens, the electron is forced to descend to a lower-energy allowed state, either the ground state or some allowed state between where it starts and the ground state. In either case, to make this transition down, the electron must emit a photon with energy once again equal to the difference between the energies of the starting and final allowed orbits (see Figure 3-52b).

92

The emitted photons have the same set of wavelengths as the absorbed photons. Furthermore, the emitted photons are sent out (that is, scattered) in all directions, which creates the glowing emission line spectra of cool gases. The color of a gas depends on the atoms and molecules that it contains. Hydrogen-rich gas clouds glow red because of the H_α emission (Figure 3-53 and Figure 3-54a). Oxygen emits many green photons, so oxygen-rich gas clouds glow green (Figure 3-54b).

If an electron orbiting in a hydrogen atom encounters a photon with more than 13.6 eV, that photon is absorbed and knocks the electron completely out of orbit and away from the atom. As noted earlier in this section, this process is called photoionization. Each type of atom and molecule has a different photoionization energy, above which all electrons are kicked out of the atom or molecule. Photoionization occurs in stars and interstellar nebulae. Indeed, many spectral lines from stars and nebulae are those of ionized atoms that retain at least one electron, such as the doubly ionized oxygen atoms in Figure 3-54b.

The speed of an object toward or away from us is called its radial velocity (Figure 3-55) because the motion is along our line of sight or, put another way, along the “radius” drawn from Earth to the object. Of course, the star or other object may also have a velocity perpendicular or transverse to our line of sight, like a car passing a pedestrian. Both the radial velocity and the transverse velocity are measured in kilometers per hour.

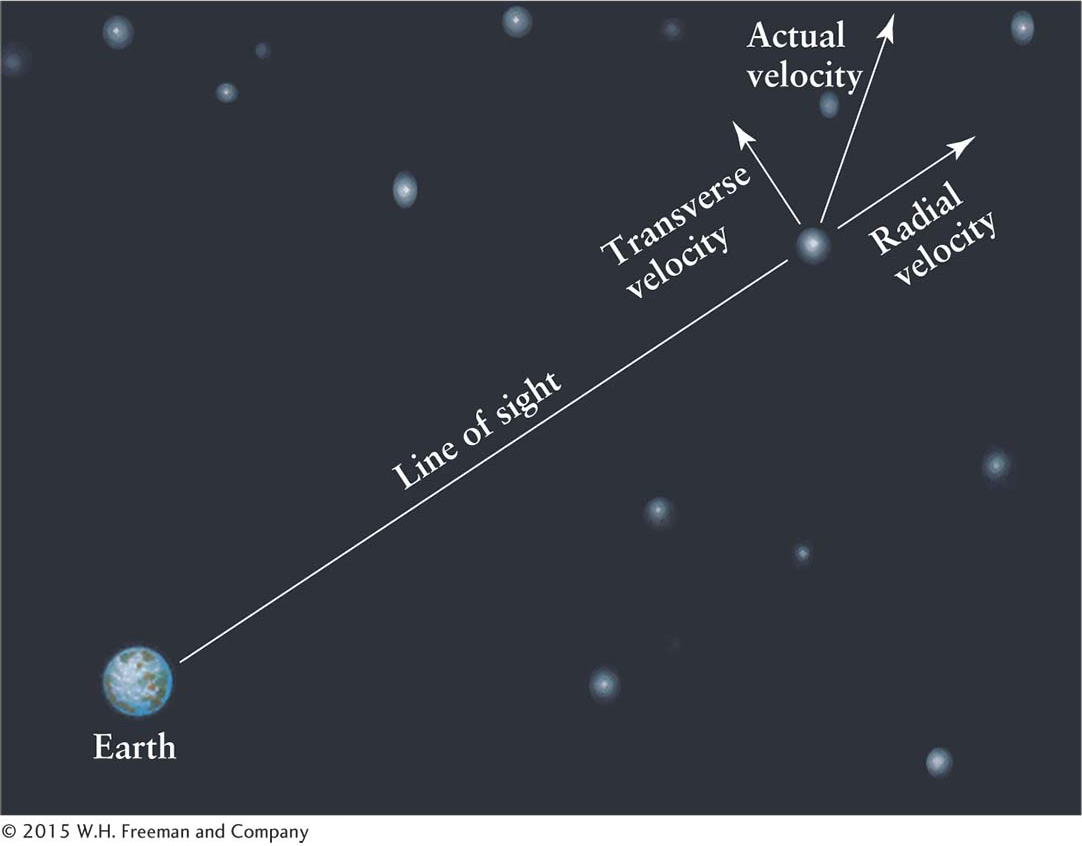
Astronomers cannot measure the transverse velocity directly. Instead they measure the angle that the body moves among the more distant stars on the celestial sphere, which appear to move much less rapidly than do stars that are closer to us. This angle is called its proper motion and is often a matter of arcseconds per year or arcseconds per century. Proper motion does not affect the perceived wavelength of an object observed here on Earth and so proper motion cannot be determined by Doppler shift (recall section 3.2). The star with the greatest proper motion as seen from Earth is Barnard’s star (Figure 3-56). Planets moving among the relatively fixed stars on the celestial sphere are examples of bodies that have large proper motions.

Stellar proper motions are so small that they can be measured for only relatively nearby stars in our Galaxy. However, the radial velocity of virtually every object in space can be determined. Indeed, even the slow motions of rising and sinking gases on the Sun’s surface can be measured by their spectral Doppler shifts. Doppler shift measurements of stars in double star systems give crucial data about the speeds of the stars orbiting each other. Doppler measurements of planets, the Sun, and other stars reveal that many of these bodies are rotating. Rotation is deduced when the Doppler shift shows that half of a surface is heading toward us, while the other half is simultaneously moving away from us. Furthermore, Doppler measurements reveal that all of the very distant galaxies are moving away from us, meaning that the universe is expanding. The spectra of distant galaxies enable us to determine the rate of that expansion. In later chapters, we will refer to the Doppler shift whenever we need to convert an observed wavelength shift into a speed toward or away from us.

93

With knowledge of spectroscopy, atomic and nuclear physics, and the Doppler shift, we can now list many of the vital properties of matter in space that are directly available to us from telescopic observations. These properties include the chemical compositions of stars, interstellar gas clouds, and other objects; the temperatures of these objects; the rotation of objects in space; the motion of objects toward or away from Earth; the presence of planets and dim companion stars; and the rate at which the universe is expanding. Knowing these properties, astrophysicists have developed and tested models that provide insights into the ages, masses, distances, internal activity, rotation rates, and companion objects of stars, among many other things.

Modern physics was born when Newton set out to understand the motions of the planets. Two and a half centuries later, scientists—including Maxwell, Planck, Einstein, Curie, Rutherford, and Doppler, among many others—discovered the basic properties of electromagnetic radiation and the structures of atoms. As we will see in the following chapters, the fruits of their labors have important implications for astronomy even today.

94