It often helps our understanding of complex topics, like planets, to see the big picture of how the major bodies are related to each other before exploring these objects in detail. To this end, we begin studying the eight planets in our solar system by comparing their physical properties. With this broad perspective in hand, we will then examine each planet and its accompanying moons individually. Earth and the three planets similar to it in chemistry, Mercury, Venus, and Mars, are studied in this chapter, whereas the larger planets, which are rock and metal (Earthlike) planets surrounded by substantial volumes of hydrogen, helium, and water, are explored in Chapter 7.

OrbitThe planets that newly forming the accretion of planetesimals in the young solar system were Mercury, Venus, Earth, Mars, Jupiter, Saturn, Uranus, and Neptune. As noted in Section 4-9 and Table 6-1, they all have similar orbital properties in that they all orbit the Sun in the same direction and in nearly the same plane (low orbital inclination). Note that, except for Mercury, their low orbital eccentricities mean that their orbits are nearly circular.

SizeThe planets fall into three size groups (Figure 6-1). The four inner planets form one group; Jupiter and Saturn, the gas giants, form the second group; and Uranus and Neptune, the ice giants, comprise the third, intermediate-size group. Jupiter is the largest planet, with a diameter about 11 times bigger than that of Earth, whereas Mercury, with about a third of Earth’s diameter, is the smallest planet. Indeed, two moons, Ganymede and Titan, are larger than Mercury. Neptune and Uranus are each about 4 times larger in diameter than Earth, the largest of the four inner planets. The diameters of the planets are given in Table 6-2.

* Pound (lb), as used here and most other places throughout this book, is a measure of mass, rather than weight.

MassA measure of the total amount of matter an object contains, its mass, is another characteristic that distinguishes the inner planets from the outer planets. The unit of mass in the metric system we use in this book is the kilogram. A slight complication occurs in describing mass in U.S. customary units. In those units the standard of mass is the slug, which is rarely used. Rather, we use the other unit of mass in U.S. customary units, the pound (lb, sometimes called the pound-mass). The confusion arises because the pound is also the common unit of weight. Weight is the force with which an object pushes down on a scale, while mass, as just mentioned, is a measure of the number and kind of particles an object possesses. In this text, pound will indicate mass when it is used following units of kilograms (kg) or when used in describing density (lb/yd³). Planetary masses are determined by measuring the periods of moons’ orbits or, for planets without moons, the gravitational effect of the planets on the orbits of passing objects. This information is used in Kepler’s third law (or similar equations) to determine the planets’ masses. The four inner planets have small masses compared to the giant outer ones. Again, first place goes to Jupiter, whose mass is 318 times greater than Earth’s mass (see Table 6-2). Uranus and Neptune, ice giants, have masses intermediate between the terrestrial and the gas giant planets.

127

128

DensitySize and mass can be combined in a useful way to provide information about the chemical composition of a planet (or any other object). Matter composed of heavy elements, such as iron or lead, has more particles (protons and neutrons) and, hence, more mass packed into the same volume than does matter composed of light elements, such as hydrogen, helium, or carbon. Therefore, objects made primarily of heavier elements have a greater average density than objects composed primarily of lighter elements, where average density is given by the equation

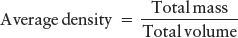
The chemical composition (kinds of elements) of any object determines its average density—how much mass the object has in a unit of volume. For example, a kilogram of rock takes up less space (is denser) than a kilogram of sugar, even though both have the same mass. Average density in metric units is expressed in kilograms per cubic meter (kg/m³). Common practice in the United States is to define density as pound/volume, such as lb/yd³, where pound here denotes mass, as discussed in the section on mass. For example, water has a density in metric units of 1000 kg/m³, which corresponds to roughly 1700 lb/yd³ in U.S. customary units. We will always present metric, and usually U.S. customary, numbers throughout the book.

To make the density of astronomical objects more comprehensible, it is often helpful to mentally compare these values with that of water, given above. The four inner planets have high average densities compared to water (see Table 6-2). In particular, the average density of Earth is 5520 kg/m³ (9300 lb/yd³). Because the density of typical surface rock is only about 3000 kg/m³ (5100 lb/yd³), this high density implies that Earth contains large amounts of material inside it, such as iron and nickel, which are much denser than surface rock.

In sharp contrast, Jupiter, Saturn, Uranus, and Neptune have relatively low average densities (see Table 6-2). Indeed, Saturn’s average density is less than that of water. The low densities of the giant outer planets suggest that they contain significant amounts of the lightest elements, hydrogen and helium, as discussed in Chapter 3. As we saw in Section 4-3, Jupiter and Saturn share similar compositions, being primarily hydrogen and helium, while Uranus and Neptune both contain vast quantities of water and ammonia, as well as much hydrogen and helium. These four worlds are sometimes called Jovian planets (the Roman god Jupiter was also known as Jove), because, like Jupiter, they all have relatively low densities and high masses compared to Earth. However, the differences in the chemistries of Jupiter and Saturn compared to those of Uranus and Neptune make the name giant planets (giant compared to Earth) more appropriate in collectively describing these four. As noted earlier, Jupiter and Saturn are specifically called gas giants, while Uranus and Neptune are ice giants.

SpectraFurther information about the chemical composition of bodies in the solar system is obtained from their spectra. For solar system objects, spectra are provided primarily by sunlight scattered off their surfaces or the clouds that surround them. As we saw in Chapter 3, spectra provide us with details of an object’s surface (or atmospheric) chemical composition and rotation rate. From their spectra, we can confirm that the outer layers of the giant planets are primarily hydrogen and helium and that the surface of Mars is rich in iron oxides, among many other things.

AlbedoThe surfaces or the upper cloud layers of the various planets scatter (send in all directions) different amounts of light. The fraction of incoming light returning directly into space is called a body’s albedo. An object that scatters no light has an albedo of 0.0; for example, powdered charcoal has an albedo of nearly 0.0. An object that scatters all of the light that strikes it (a high-quality mirror comes close) has an albedo of 1.0. Multiplying the albedo of an object by 100 gives the percentage of light directly scattered off that body. Three planets (Mercury, Earth, and Mars) have albedos of 0.37 or less. Such albedos result from dark, dry surfaces or from a mixture of light (water and clouds) and dark surfaces (continents) exposed to space. In contrast, Venus, Jupiter, Saturn, Uranus, and Neptune have albedos of 0.47 or more. High albedos like these imply bright materials exposed to space. The albedos of these latter five planets are high because they are all completely enshrouded by clouds, which scatter sunlight back into space very efficiently.

MoonsEvery planet, except Mercury and Venus, has moons. At least 173 planetary moons are known to exist in the solar system (up from 99 known in 2001), and more are still being discovered. Table 6-3 lists the numbers of moons orbiting each planet. Unlike our Moon, most moons are irregularly shaped, and look more like potatoes than spheres. We will discover that there is as much variety among moons as there is among planets.

129