Example 16

EXAMPLE 16 $Z$ test for $p_{1} - p_{2}$ using the $p$ -value method

The General Social Survey tracks trends in American society through annual surveys. Married respondents were asked to characterize their feelings about being married. The results are shown here in a crosstabulation with gender. Test the hypothesis that the proportion of females who report being very happily married is smaller than the proportion of males who report being very happily married. Use the $p$ -value method with level of significance $α = 0.05$ .

marriage

	Very happy	Pretty happy/ Not too happy	Total
Female	257	166	423
Male	242	124	366
Total	499	290	789

Solution

From the crosstabulation, we assemble the statistics in Table 15 for the independent random samples of men and women.

Table 10.52: Table 15 Sample statistics of very happily married respondents

	Sample size	Number very happy	Sample proportion very happy
Females (sample 1)	$n_{1} = 423$	$x_{1} = 257$	${\hat{p}}_{1} = \frac{x_{1}}{n_{1}} = \frac{257}{423} \approx 0.6076$
Males (sample 2)	$n_{2} = 366$	$x_{2} = 242$	${\hat{p}}_{2} = \frac{x_{2}}{n_{2}} = \frac{257}{423} \approx 0.6612$

We first check whether the conditions for the $Z$ test are valid: $x_{1} = 257 \geq 5$ , $(n_{1} - x_{1}) = (423 - 257) = 166 \geq 5$ , $x_{2} = 242 \geq 5$ , and $(n_{2} - x_{2}) = (366 - 242) = 124 \geq 5$ . We can therefore proceed.

Step 1 State the hypotheses and the rejection rule.

We are interested in whether the proportion of females who report being very happily married is smaller than that of males and because the females represent sample 1, the hypotheses are

$\begin{matrix} H_{0} : p_{1} = p_{2} & H_{a} : p_{1} < p_{2} \end{matrix}$

Page 612

where $p_{1}$ and $p_{2}$ represent the population proportions of all females and males, respectively, who report being very happily married. We will reject $H_{0}$ if the $p - value \leq α = 0.05$ .

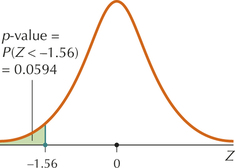FIGURE 18 $p$ -Value for left-tailed $Z$ test.
Step 2 Find $Z_{data}$ .

First, use the data from Table 15 to find the value of ${\hat{p}}_{pooled}$ .

${\hat{p}}_{pooled} = \frac{x_{1} + x_{2}}{n_{1} + n_{2}} = \frac{257 + 242}{423 + 366} \approx 0.63245$

Then

$Z_{data} = \frac{(0.6076 - 0.6612)}{\sqrt{0.63245} \cdot (1 - 0.63245) (\frac{1}{423} + \frac{1}{366})} \approx - 1.56$
Step 3 Find the $p$ -value.

Because it is a left-tailed test, the $p$ -value is given by Table 14 as $P (Z < Z_{data}) = P (Z < - 1.56)$ , as shown in Figure 18. This amounts to a Case 1 problem from Table 8 in Chapter 6 on page 357:

$P (Z < - 1.56) = 0.0594$
Step 4 State the conclusion and the interpretation.

The $p -value = 0.0594$ is not less than or equal to $α = 0.05$ , so we do not reject $H_{0}$ . There is insufficient evidence that the proportion of females who report being very happily married is smaller than the proportion of males who do so.

Note: When the $p$ -value is close to $α$ , many data analysts prefer to simply assess the strength of evidence against the null hypothesis using criteria such as those given in Table 6 in Chapter 9 (page 514).

NOW YOU CAN DO

Exercises 9–12.