Example 20

EXAMPLE 20 $F$ test for comparing two population standard deviations: Critical-value method

Table 18 shows independent samples from Google and Apple stock prices from July 2014 together with the sample sizes and sample standard deviations. Test, using the critical-value method, whether the standard deviation of Google stock prices $σ_{1}$ is greater than the standard deviation of Apple stock prices $σ_{2}$ .

Table 10.62: Table 18 Independent random samples of stock prices, July 2014

Google	Apple
574.79 590.76 583.04 593.06 580.82 599.02 579.55 587.78	93.52 94.03 95.39 96.45 95.60 99.02 97.03
$\begin{matrix} n_{1} = 8 & s_{1} \approx 7.999701 \end{matrix}$	$\begin{matrix} n_{2} = 7 & s_{2} \approx 1.862594 \end{matrix}$

Table 10.62: Source: www.marketwatch.com/tools/quotes/historical.asp.

Solution

The normal probability plots in Figures 22a and 22b show acceptable normality for both samples. We may, therefore, proceed with the $F$ test for comparing population standard deviations.

FIGURE 22a Normal probability plot of Google stock prices.

FIGURE 22b Normal probability plot of Apple stock prices.

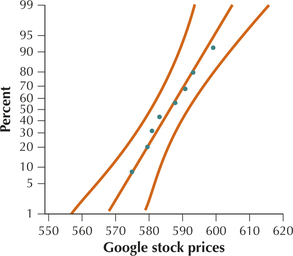
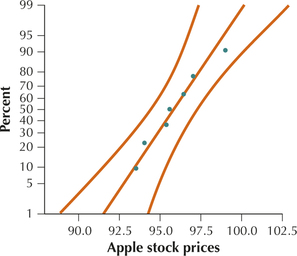
Step 1 State the hypotheses. We are testing whether Google's stock prices are more variable than those of Apple. Thus, because Google represents population 1, we have the following hypotheses for our $F$ test:

$\begin{matrix} H_{0} : σ_{1} = σ_{2} & versus & H_{a} : σ_{1} > σ_{2} \end{matrix}$

where $σ_{1}$ represents the standard deviation of Google stock prices and $σ_{2}$ represents the standard deviation of Apple stock prices. Use level of significance $α = 0.05$ .
Step 2 Find the critical value and state the rejection rule. We have ${df}_{1} = n_{1} - 1 = 7$ and ${df}_{2} = n_{2} - 1 = 6$ . From Table 17 and Appendix Table F, our critical value is the $F$ -value with area $α = 0.05$ to the right of it:

$F_{crit} = F_{α, n_{1} - 1, n_{2} - 1} = F_{0, 0.5, 7.6} = 4.21$

Our rejection rule is, therefore, from Table 17: Reject $H_{0}$ if $F_{data} > 4.21$ .

Page 623
Step 3 Find $F_{data}$

$F_{data} = \frac{S_{1}^{2}}{S_{2}^{2}} = \frac{{7.999701}^{2}}{{1.862594}^{2}} \approx 18.45$

follows an $F$ distribution with ${df}_{1} = n_{1} - 1 = n_{1} - 1 = 7$ and ${df}_{2} = n_{2} - 1 = n_{2} - 1 = 6$ .
Step 4 State the conclusion and the interpretation. Because $F_{data} \approx 18.45$ is greater than $F_{crit} = 4.21$ , we reject $H_{0}$ . There is evidence that the variability in Google stock prices is greater than the variability in Apple stock prices.

NOW YOU CAN DO

Exercises 21–26.