EXAMPLE 21 Test for comparing two population standard deviations: -value method

The Web site Medicare.gov publishes survey information on patient attitudes about their level of care. Table 20 shows the percentages of respondents taken from independent random samples of hospitals in Florida and Georgia, which reported that their nurses always communicated well.

624

Table 10.64: Table 20 Independent random samples of hospital percentages
Florida Georgia
67 66 70 70 72 73 72 75 78 73 68 71
63 69 65 68 65 82 72 77 75 73
Table 10.64: Source: Medicare.gov.

Test whether there is a difference in variability between the two states, using .

Solution

Because the normal probability plots in Figures 23a and 23b show acceptable normality, we may therefore proceed with the test for comparing population standard deviations.

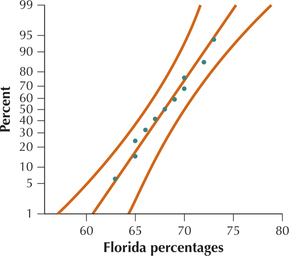
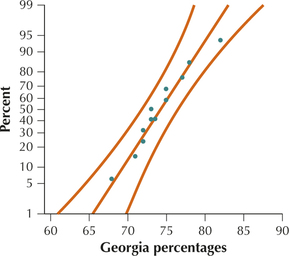
image
Figure 10.24: FIGURE 23a Normal probability plot of Florida percentages.
image
Figure 10.25: FIGURE 23b Normal probability plot of Georgia percentages.

  • Step 1 State the hypotheses. We are testing whether there is a difference in the standard deviation of the percentages for Florida () and Georgia (). We therefore have a two-tailed test:

    where and represent the standard deviations of the percent of Florida and Georgia respondents, respectively, who reported that their nurses always communicated well. Use level of significance .

  • Step 2 Find .

    follows an distribution with and .

  • Step 3 Find the -value. Because we have a two-tailed test, Table 19 states that the -value is

    Figure 24a shows the output from the TI-83/84, giving as the area under the distribution curve between 0.6729 and infinity. This gives

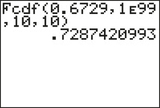    image
    Figure 10.26: FIGURE 24a

    This cannot represent a valid -value, because it is larger than 1. Figure 24b shows the output from the TI-83/84, giving as the area under the distribution curve between 0 and 0.6729. Thus, our -value is:

    because this is smaller than 1.457484199.

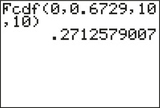    image
    Figure 10.27: FIGURE 24b

    625

  • Step 4 State the conclusion and the interpretation. The -value 0.5425 is not less than , so we do not reject . There is insufficient evidence for a difference in population standard deviations between percentages of patients in Florida and Georgia hospitals who reported that their nurses always communicated well.

NOW YOU CAN DO

Exercises 27–32.