Example 7

EXAMPLE 7 $t$ Test for $μ_{1} - μ_{2}$ : Critical-value method

Using Table 7, test whether women's population mean body temperature differs from that of men, using the critical-value method and $α = 0.05$ .

Solution

Both sample sizes are large ( $n_{1} = n_{2} = 65 \geq 30$ ), so we can perform the hypothesis test.

Page 592

Step 1 State the hypotheses.

The key words “differs from” indicate a two-tail test:

$\begin{matrix} H_{0} : μ_{1} = μ_{2} & versus & H_{a} : μ_{1} \neq μ_{2} \end{matrix}$

where $μ_{1}$ and $μ_{2}$ represent the population mean body temperature for women and men, respectively.
Step 2 Find $t_{crit}$ and state the rejection rule.

The required degrees of freedom is the smaller of $n_{1} - 1$ and $n_{2} - 1$ , which is $65 - 1 = 64$ . Unfortunately, $df = 64$ is not in the $t$ table in Appendix Table D, so we use the conservative $df = 60$ . For $α = 0.05$ , this gives $t_{crit} = 2.000$ . We have a two-tailed test, so Table 8 gives us the following rejection rule:

$Reject H_{0} if t_{data} \geq 2.000 or t_{data} \leq - 2.000$
Step 3 Find $t_{data}$ .
$t_{data} = \frac{({\bar{x}}_{1} - {\bar{x}}_{2})}{\sqrt{\frac{s_{1}^{2}}{n_{1}} + \frac{s_{2}^{2}}{n_{2}}}} = \frac{(98.394 - 98.105)}{\sqrt{\frac{{(0.743)}^{2}}{65} + \frac{{(0.699)}^{2}}{65}}} \approx 2.28$
Step 4 State the conclusion and the interpretation.

The test statistic $t_{data} = 2.28$ is greater than $t_{crit} = 2.000$ (see Figure 11). We therefore reject $H_{0}$ . There is evidence, at level of significance $α = 0.05$ , that the population mean body temperatures are not the same for women and men.

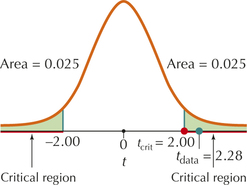FIGURE 11 $t_{data} = 2.28$ falls within the critical region.

NOW YOU CAN DO

Exercises 3–6.