Example 5

EXAMPLE 5 p-Value method for the $χ^{2}$ goodness of fit test using technology

Table 5 contains the distribution of violent crime in New York City in 2012.² Suppose that a random sample of 1000 violent crimes in New York City yielded the counts shown in Table 6. Test whether the population proportions have changed since 2012, using the p-value method and level of significance $α = 0.05$ .

Table 11.5: Table 5 2012 violent crime in New York City

Murder	Rape	Robbery	Assault
0.01	0.04	0.35	0.60

Page 640

Table 11.6: Table 6 Sample of 1000 violent crimes in New York City this year

Murder	Rape	Robbery	Assault
6	50	350	594

Solution

Step 1 State the hypotheses and the rejection rule. Check the conditions.
$\begin{array}{l} H_{0} : p_{Murder} = 0.01, p_{Rape} = 0.04, p_{Robbery} = 0.35, p_{Assault} = 0.60 \\ H_{a} : The random variable does not follow the distribution specified in H_{0} \end{array}$

Reject $H_{0}$ if the p-value $\leq 0.05$ .

What Results Might We Expect?

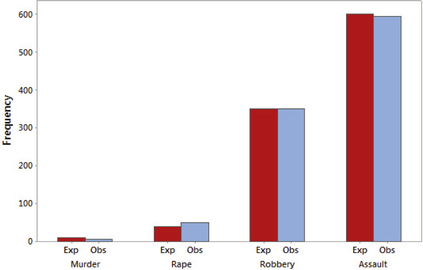
Before we do the formal hypothesis test, let's try to figure out what the conclusion might be. Figure 4 is a clustered bar graph (see Section 2.1) of the observed and expected frequencies for each of the four categories. If $H_{0}$ were true, then, for each category, we would expect the red bars (observed frequencies) and blue bars (expected frequencies) to have somewhat similar heights. In fact, the heights of the bars are fairly similar for all four categories, indicating not much difference between the crimes that were observed and the crimes that were expected. Thus, we might expect to not reject $H_{0}$ .

FIGURE 4 Graph indicates no evidence against

$H_{0}$ .

First, we need to find the expected frequencies. We have $n = 1000$ , so the expected frequencies are as shown here.

Category	$E x p e c t e d f r e q u e n c y_{i} = E_{i} = n \cdot p_{i}$
Murder	$E_{Murder} = 1000 \cdot 0.01 = 10$
Rape	$E_{Rape} = 1000 \cdot 0.04 = 40$
Robbery	$E_{Robbery} = 1000 \cdot 0.35 = 350$
Assault	$E_{Assault} = 1000 \cdot 0.60 = 600$

Table 11.7: Expected frequencies for violent crimes in a sample of size

$n = 1000$

Page 641

Next, check the conditions for this test. Because (a) none of the expected frequencies is less than 1 and (b) no more than 20% of the expected frequencies are less than 5, we may proceed. We use the instructions provided in the Step-by-Step Technology Guide at the end of this section.

Step 2 Find the test statistic $χ_{data}^{2}$ . The TI-83/84 results in Figure 5 tell us that

$χ_{data}^{2} = 4.16$
Step 3 Find the p-value. Figure 5 also tells us that

$p -value = P (χ^{2} > 4.16) = 0.2446972817 \approx 0.2447$

This p-value, for the χ² distribution with 3 degrees of freedom, is shown in Figure 6.

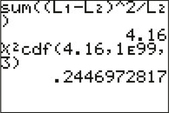FIGURE 5 $χ_{data}^{2} = 4.16$ has p-value 0.2447.

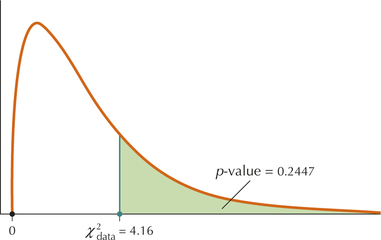FIGURE 6

Figure 7a shows the TI-84 output for the test, and Figure 7b shows the SPSS output for the test, confirming our test statistic of 4.16 and p-value of 0.2447.

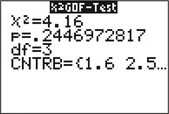FIGURE 7a $χ^{2}$ test on TI-84.

FIGURE 7b $χ^{2}$ test in SPSS.
Step 4 State the conclusion and the interpretation. The p-value is not less than $α = 0.05$ , so we do not reject $H_{0}$ , which we expected. There is insufficient evidence, at a level of significance $α = 0.05$ , that the population proportions of violent crime have changed in New York City since 2012.

NOW YOU CAN DO

Exercises 23–26.