$\begin{array}{lll}{H}_0:{\mu }_{\mathrm{A}}={\mu }_{\mathrm{B}}={\mu }_{\mathrm{C}}\hfill & \text{versus}\hfill & H_a:\text{not all the population means are equal}\hfill \end{array}$

• Step 1 Normality. To verify that each of the $k=3$ populations is normally distributed, we examine normal probability plots of each sample, shown in Figure 5. Each plot indicates acceptable normality.

  FIGURE 5 Normal probability plots verify normality requirement.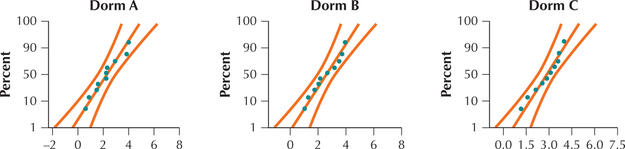

  
  Page 670

• Step 2 Equal Variances. To find the standard deviation for Dorm A, we first find

  $\begin{array}{l}{{\displaystyle \sum {(x-\overline{x})}^2=(0.60-2.2)}}^2+(3.82-2.2{)}^2+(4.00-2.2{)}^2+(2.22-2.2{)}^2\\ +(1.46-2.2{)}^2+(2.91-2.2{)}^2+(2.20-2.2{)}^2+(1.60-2.2{)}^2\\ +(0.89-2.2{)}^2+(2.30-2.2{)}^2\\ =11.5626\end{array}$

  Then

  $s_{\mathrm{A}}=\sqrt{\frac{{\displaystyle \sum {(x-\overline{x})}^2}}{n-1}}=\sqrt{\frac{11.5626}{10-1}}\approx 1.133460777$

  We similarly find $s_{\mathrm{B}}\approx 1.030857248$ and $s_{\mathrm{C}}\approx 0.9370284$. The largest, $s_{\mathrm{A}}\approx 1.133460777$, is not larger than twice the smallest, $s_{\mathrm{C}}\approx 0.9370284$. Thus, the equal variance require-ment is satisfied.

• Step 3 Independence. Because the students are randomly sampled from each dormitory, with the selection of students in one dormitory not affecting the selection of students sampled from the other dormitories, the independence assumption is also validated.